Выбор уравнения для описания формы продольного профиля с запасом металла на износ в пределах зоны перекатывания

• Вывод расчётной формулы для построения возвышения профиля крестовины на основе параболы 7-й степени
• Вывод приближенной расчётной формулы для построения возвышения профиля крестовины на основе уравнения параболы 3-й степени.
• Оценка приближенности зеркального повторения кривой износа для различных профилей крестовины
• Построение поперечных профилей крестовин с запасом металла на износ
• Выводы по главе

Форма возвышения в наиболее изнашиваемом участке выполнена по кривой, согласно уравнения 4.2. Схематично кривая возвышения показана на рисунке.

• где у — ордината кривой 6 в любой точке;
• Х- абсцисса расчетного сечения;
• х₀ — расстояние от сечения 5 сердечника 1, равного ширине головки рельса до сечения 7, в котором регламентирован допуск износ крестовины;
• £> — допуск на вертикальный износ крестовины;
• е — основание натурального логарифма.

По уравнению показательной функции 4.1. построена кривые возвышения для различных расчётных сечений крестовины марки 1/9 типа рельса Р65 (Приложение 5) и для последующей количественной оценки запаса металла посчитана площадь возвышения продольного профиля (Приложение 6).

Рисунок 4.2 — Крестовина для рельсовых пересечений а) вид в плане; б) продольный профиль Сущность технического решения разъясняется с помощью чертежа

(рис. 4.2), на котором приведены общий вид крестовины в плане и продольные профили предлагаемой конструкции и прототипа на участке между сечением сердечника, равным ширине головки рельса, и горлом крестовины. Для наглядности эти профили нанесены утрировано с увеличением вертикального масштаба по отношению к горизонтальному.

Крестовина содержит сердечник 1 и два усовика 2 и 3, образующие горло 4. Ее участок Ь, заключенный между сечением 5, в котором сердечник 1 равен ширине головки рельса, и сечением горла 4 крестовины выполнен с возвышением продольного профиля.

Анализ функции (4.1) позволил выявить ряд её недостатков:

• Не трудно убедиться, что первая производная данного выражения при х=0 не обращается в ноль. Это значит, что в начале координат кривая пересекает ось х под некоторым углом а. Таким образом, вертикальная неровность в виде угла а заложена в самом уравнении, не обеспечивающем плавного сопряжения прямолинейного и криволинейного участков профиля.
• Само уравнение не содержит ни одного свободного параметра, варьируя которым, мы можем оптимизировать форму кривой.
• И наконец, расчётная формула, в которой абсциссы х и х₀ входят в выражение показателя степени основания натурального логарифма е, создает определенные затруднения в её использовании при проектировании.

В поисках функции для описания конфигурации возвышения продольного профиля, не обладающей указанными недостатками, за основу была принята параболическая зависимость.

На рис 4.2, б схематично показаны две кривые возвышения: кривая 6, построенная по уравнению показательной функции (ур-е 4.1) и кривая 8, построенная по уравнению параболической функции, использование которой является целесообразным с точки зрения плавности входа экипажа на возвышение и схода с него.

Использование параболической функции позволяет спроектировать кривую возвышения продольного профиля с плавным входом экипажа на возвышение и сходом с него. В поисках оптимальной формы возвышения продольного профиля с точки зрения точности повторения кривой износа по количественному анализу запаса металла (см. раздел 4.4) и простоты математических вычислений разработаны три формы продольного профиля, построенные на основе парабол 7-й, 5-й и 3-й степени. Степень уравнения определялась количеством исходных условий.

Вывод расчётной формулы для построения возвышения профиля крестовины на основе параболы 7-й степени

Исходными данными при выводе расчётной формулы для построения возвышения продольного профиля являются геометрические размеры крестовины, допуск на вертикальный износ крестовины и радиус входа колеса подвижного состава на возвышение. Как показали экспериментальные наблюдения конструкций прототипов, радиус входа является важным параметром. При радиусе входа, меньшем радиуса колеса наблюдался более интенсивный износ, чем износ крестовин традиционной крестовины и на поверхности крестовины кроме основной неровности типа впадины, появлялись еще локальные неровности, которые негативным образом сказывались на прохождении экипажа стрелочного перевода. В этой связи была поставлена задача разработки уравнения кривой, в которой дополнительно учтено условие: радиус Я входа на возвышение должен быть не менее радиуса экипажа.

Величина допуска на вертикальный износ зависит от нормы допускаемого износа поверхности крестовины.

Разработана конструкция крестовины с запасом металла на износ [69], включающая в себя все перечисленные выше исходные данные, возвышение продольного профиля которой описывается уравнением 4.2.

где:

• у — ордината продольного профиля в расчётном сечении;
• х — расстояние от сечения сердечника, равного ширине головки рельса до расчётного сечения;
• Хо — расстояние от сечения сердечника, равного ширине головки рельса до сечения, в котором регламентирован допуск крестовины на вертикальный износ;
• В — допуск на вертикальный износ крестовины;
• Ь — расстояние от сечения сердечника равного ширине головки рельса до горла крестовины.
• Я — радиус возвышения профиля в месте его сопряжения с передним и задним вылетами крестовины.

Форма возвышения продольного профиля крестовины с запасом металла на износ описана параболой 7-й степени с 8-ю коэффициентами, т.к. для кривой были заданы 8 начальных условий.

Крестовина с запасом металла на износ (рис. 4.4), содержит сердечник 1 и два усовика 2, образующие горло крестовины, а также передний и задний вылеты 3. На участке зоны перекатывания от горла 4 до сечения сердечника, равного ширине головки рельса 5 крестовина выполнена с возвышениями 6 и 7, соответственно усовиков 2 и сердечника 1 для обеспечения запаса металла на износ.

Рисунок 4.4- Крестовина для рельсовых пересечений (а — вид в плане, б — продольный профиль крестовины) По полученной формуле для различных расчётных сечений были получены ординаты возвышения продольного профиля (Приложение 2).

Для расчёта была выбрана крестовина марки 1/9. Допуск на вертикальный износ принят равным 10 мм, исходя из нормы допускаемого износа для приемоотправочных путей. Радиус входа экипажа на возвышения принят равным 1280 мм. Это значение было получено методом подбора (Приложение 1). Сводный график продольных профилей при различных радиусах входа представлен на рис. 4.4. При радиусе входа 11=1280 мм кривая имеет одну точку экстремума в расчётном сечении. При других значениях радиуса входа наблюдаются экстремальные значения, значительно большие, чем допуск на вертикальный износ V = 10 мм, принятый для сеч. 12 (практический центр крестовины). При радиусе 11=1280 мм в соседних с расчётным сечениях наблюдаются значения, большие чем допуск на вертикальный износ.

Однако, при округлении значений до целого для последующего проектирования крестовины этими отклонениями можно пренебречь.

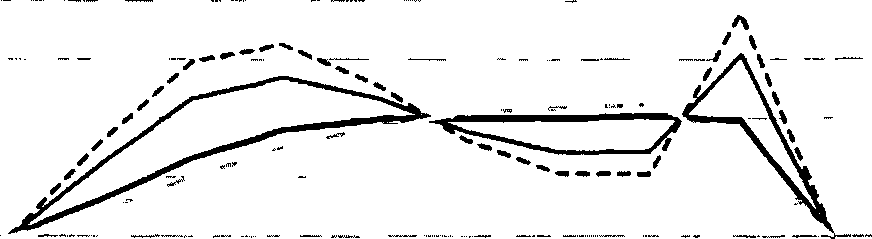
Рисунок 4.4 — Графики кривой возвышения, рассчитанной по уравнению 4 2, при различных радиусах входа

Радиус входа на возвышение 11=1280 мм больше чем радиус колеса подвижного состава (11=450 мм) Тем самым выполняется условие плавного входа экипажа на возвышение и схода с него, что благоприятно скажется на равномерности износа поверхности крестовины без образования промежуточных локальных неровностей (рис 4.5), связанных с скачкообразным входом колеса на бугор при радиусе колеса большем, чем радиус входа на возвышение.

По формуле 4.2 выполнен расчёт ординат возвышения для различных расчётных сечений крестовины, в каждом из которых регламентировался допуск на вертикальный износ 0=1 Омм. Результаты расчёта (Прил.2) показали возможность использования данного уравнения при проектировании крестовин с запасом металла на износ с максимальной точкой возвышения в сечениях 20, п.ц.к. и м.ц.к.

Основным недостатком крестовины с запасом на износ, ординаты возвышения которой могут быть определены по формуле 4.2, является сложность математических вычислений. Определение ординат возможно только при помощи специально разработанной программы. При вычислении ординат, не прибегая к помощи ЭВМ, велика вероятность арифметических ошибок.

Доказав, что для построения кривой запаса металла необходимо задать радиус входа больший чем радиус колеса, следующим шагом при проектировании уравнения кривой встала задача упрощения уравнения. Для этого было решено отказаться от параметра К — радиуса входа колеса на возвышение, тем самым сократив количество начальных условий до 6-ти и получив уравнение параболы 5-й степени.

Как видно из уравнения возвышения продольного профиля ордината у зависит от геометрических параметров крестовины (т.е. марки крестовины) и запаса металла на износ D. Для крестовины марки 1/9 типа Р65 были проведены расчёты форм возвышения с максимальным запасом на износ в различных расчётных сечениях (Приложение 3). Допуск на вертикальный износ принят равным 10 мм, исходя из нормы допускаемого износа для приемоотправочных путей (см. табл. 2.1).

Кривая возвышения с максимальным запасом металла на износ в практическом центре крестовины (сеч. 12) приведена на рисунке 4.7.

Следует отметить, что в целях наглядности изображения формы кривой возвышения продольного профиля, вертикальный и горизонтальные масштабы не соответствуют. Анализируя результаты расчёта можно наблюдать плавное увеличение значений ординат продольного профиля от нуля до величины регламентированного допуска на вертикальный износ В, принятого 10 мм для сечения п.ц.к.

Как видно из результатов расчёта кривой (приложение 3) предложенная формула универсальна и по ней могут быть рассчитаны кривые для различных расчётных сечений. В зависимости от величины средневзвешенного износа бандажей колесных пар допуск на вертикальный износ может быть регламентирован для различных расчётных сечений. Но, исходя из необходимости плавного нарастания ординат кривой возвышения до величины й и плавного уменьшения ординат до нулевого значения, можно сделать вывод, что по уравнению 4.3 кривая запаса металла на износ может быть построена для сечений 12 (п.ц.к.) и м.ц.к.

Несмотря на упрощение уравнения за счёт отказа от параметра радиуса входа на возвышение, уравнение кривой возвышения 4.3 в конечном виде остаётся сложным для расчёта кривых. Следующим шагом в выводе формулы описания кривой возвышения продольного профиля была разработка нового метода построения кривых. Если раньше вся кривая возвышения рассматривалась целиком, как одна парабола, и строилась от пулевой точки, то в новом методе кривая состоит из двух парабол, которые строятся с двух сторон рассматриваемого участка крестовины и соединяются в расчётном сечении с максимальным допуском на вертикальный износ. За счёт применения нового метода составных парабол удалось существенно понизить порядок уравнения до 3-й степени, тем самым значительно упростить уравнение кривой.

Вывод приближенной расчётной формулы для построения возвышения профиля крестовины на основе уравнения параболы 3-й степени.

В целях повышения надёжности алгоритма расчёта и упрощения математического аппарата нами была предложено уравнение параболы 3-й степени (ур-е 4.4) и новый метод составных парабол для построения кривой возвышения продольного профиля:

у = а_хх^ъ + а₂х², (4.4)

• где у — ордината продольного профиля в расчётном сечении;
• D — допуск на вертикальный износ крестовины;
• х — абсцисса расчётного сечения;
• / — абсцисса сечения, в котором регламентирован допуск крестовины на вертикальный износ;

Форма возвышения продольного профиля крестовины с запасом металла на износ описана параболой 3-й степени с 4-мя коэффициентами, т.к. для кривой были заданы 4 начальных условий:

у = а_хх^г + а₂х² + а_ъх + <з₄ (4.4)

Для определения начальных условий использовалась следующая расчётная схема (рис. 4.8):

Как видно из расчётной схемы, кривая возвышения продольного профиля строится с 2-х сторон рассматриваемого участка крестовины. Точка соединения кривых — расчётное сечение, в котором максимальный регламентирован запас металла на износ.

у = а,х³ + а₂х² + а₃х + а_л

при х = 0: у а_А = О

В отличии от уравнений кривых, построенных по уравнениям 4.2, 4.3, полученная формула является приближенной, но обеспечивающей точность расчётов в пределах точности изготовления конструкции. Она отличается простотой. Для расчёта ординат кривой не требует специальных прикладных программ и при необходимости он может быть выполнен даже в полевых условиях. В ней ордината кривой возвышения зависит только от марки крестовины и допуска на вертикальный износ в расчётном сечении.

Таблицы расчётов ординат возвышений для различных расчётных сечений представлены в приложении 4. Для сечения практического центра крестовины (сеч. 12) график возвышения продольного профиля показан на рисунке 4.9. Кривая строилась не целиком, а с 2-х сторон — от сечения головки рельса 72,8 и от горла крестовины. Две кривые соединились в расчётном сечении п.ц.к. с ординатой 10 мм (величина допуска на вертикальный износ).

Рисунок 4.9 — Таблица расчёта возвышения продольного профиля и график кривой (уравнение 4.4) при допуске на износ в сечении п.ц.к.

В приложении 4 представлены расчётные таблицы возвышения продольного профиля для различных сечений крестовины марки 1/9 типа Р65 с допуском на вертикальный износ В равным 10 мм. Результаты расчёта показали, что по предложенному уравнению кривая возвышения продольного профиля крестовины может быть построена для различных расчётных сечений, но, исходя из требования плавности нарастания ординат возвышения продольного профиля, уравнение может быть использовано для построения кривых с максимальным запасом на износ в сечении 12 и математическом центре крестовины (м.ц.к.).

Оценка приближенности зеркального повторения кривой износа для различных профилей крестовины

Основная идея предложенных конструкций крестовин с запасом металла заключается в максимальном отражении формы износа. Одним из критериев оценки приближенного зеркального повторения кривой износа принята количественная оценка запаса металла, а именно площадь под кривой. Для этого необходимо знать площадь над кривой износа и площадь под кривой запаса металла. Равенство этих площадей позволит сделать вывод о том, какая из предложенных формул позволяет построить кривую возвышения максимально точно повторяющую кривую износа поверхности катания крестовины.

Сначала была подсчитана площадь над кривой износа на предельно изношенной крестовине. По результатам исследований институтов Промтрансниипроект и ЛИИЖТ (см. рис. 2.5, 2.6) построены кривые износа поверхности крестовины при различных пропущенных тоннажах (рис. 4.10) и подсчитана площадь над кривой износа. При пропущенном тоннаже в 90 млн. тонн брутто площадь износа составила 9248 мм .

атем был выполнен расчёт площадей под кривыми запаса металла на износ для различных продольных профилей крестовины:

• крестовина с запасом металла на износ с возвышением по показательной функции (ур-е 4.1)
• крестовина с запасом металла на износ с возвышением по параболе 7- й степени (ур-е 4.2)
• крестовина с запасом металла на износ с возвышением по параболе 5- й степени (ур-е 4.3)
• крестовина с запасом металла на износ с возвышением по параболе 3- й степени (ур-е 4.4)

Расчёты площадей приведены в приложении 6, результаты сведены в таблицу 4.1.

Площадь	Площадь запаса	Площадь	Площадь	Площадь
изношенного	металла на	запаса металла	запаса металла	запаса металла
металла при	износ —	на износ —	на износ —	на износ —
пропущенном	показательная	парабола 7-й	парабола 5-й	парабола 3-й
тоннаже 90 млн.	функция	степени	степени	степени
тонн, бр., мм. кв.	(ур-е 4.1),	(ур-е 4.2),	(ур-е 4.3),	(ур-е 4.4),
	мм. кв.	мм. кв.	мм. кв.	мм. кв.
9248	10618	9345	6551	6347
Процент расхождения	12%	1%	29%	31%

Проанализировав все полученные площади запаса металла на износ, можно сделать вывод, что наиболее приближена к площади износа кривая, рассчитанная по уравнению параболы 7-й степени (уравнение 4.2).

Вторым критерием оценки точности зеркального отображения выбран сравнительный анализ ординат кривых возвышения и кривой износа. Сравнение ординат выполнено для тонких сечений сердечника крестовины, как наиболее интенсивной зоны, ввиду уменьшения площадки опирания колес на поверхность крестовины. Значения ординат кривой износа и кривых возвышения приведены в таблице 4.2.

Наименование кривой	Ордината в сечении сердечника крестовины, мм
	Сеч. 50	Сеч. 40	Сеч. 30	Сеч. 20	Сеч. 10
Кривая износа	7,4	9,3	9,55	9,8	9,9
Парабола 7-й степени	6,7	9	9,9	10,05	10
Парабола 5-й степени	4	6,5	8,5	9,7	10
Парабола 3-й степени	3,15	5,6	7,9	9,5	10

В таблице 4.3 приведены результаты расчёта разностей ординат кривой износа и кривых возвышений и определено средневзвешенной отклонение.

Наименование кривой	Относительно се		с отклонение в сечениях рдечника, мм			Средневзвешенное отклонение, мм
	Сеч. 50	Сеч. 40	Сеч. 30	Сеч. 20	Сеч. 10
Парабола 7-й степени	0,7	0,3	0,35	0,25	0,1	0,34
Парабола 5-й степени	3,4	2,8	1,05	0,1	0,1	1,49
Парабола 3-й степени	4,25	3,7	1,65	0,3	0,1	2

Сравнительный анализ ординат кривых показал, что наиболее приближена к кривой износа парабола 7-й степени. Средневзвешенно отклонение по рассматриваемым тонким сечениям сердечника составило О, 34 мм.

Как уже было сказано, главным недостатком этого уравнения является сложность математических вычислений. Ввиду этого наиболее перспективным представляется форма кривой, рассчитанная по уравнению 4.4 (кривая параболы 3-й степени). Разница между площадью износа и площадью под кривой составила 31 % (табл. 4.1) средневзвешенное отклонение ординат — 2 мм (табл. 4.3).

Построение поперечных профилей крестовин с запасом металла на износ

При проектировании поперечного профиля усовиков крестовины с запасом металла на износ необходимо определить ординаты возвышения продольного профиля сердечника. Главной особенностью проектирования продольных профилей крестовины с запасом металла на износ является форма траектории движения по ней колес, которая является базисной линией для расчёта координат профилей. У крестовин традиционных конструкций она прямолинейная по всей длине, а у крестовины с запасом металла на износ имеет возвышение на участке зоны перекатывания колес с сердечника на усовики и обратно. Кривая запаса металла на износ зеркально отображает кривую износа поверхности катания (рис. 4). В диссертации на соискание кандидатской степени представлены математические обоснования кривой возвышения.

Для каждого расчётного сечения по известным ординатам возвышения продольного профиля строятся поперечные сечения. На рисунке 4.11 показан поперечный профиль крестовины, усовик которой запроектирован с учетом средневзвешенного износа бандажа с уклоном 1:9. Запас металла 1 образован между линией уклона усовика традиционной конструкции (1:20) и линий уклона с учетом износа бандажа (1:9). В начале проектируется сердечник крестовины, в котором учитывается запас металла на износ 2. Относительно сердечника проектируется усовик крестовины с проектным уклоном поверхности катания 1:9. В результате получаем усовик с двумя возвышениями поперечного профиля: запас металла с учетом уклона износа бандажа колесной пары / и запас металла относительно сердечника крестовины с запасом металла на износ 3.

Рисунок 4.11 — Поперечный профиль крестовины с запасом металла на износ

Данная методика проектирования поперечного профиля может быть применена как для всего железнодорожного транспорта необщего пользования, так для отдельного промышленного предприятия. Во втором случае поперечный профиль может быть запроектирован под средневзвешенный износ колесных пар, обращающихся на путях необщего пользования (уклон 1:9), либо под средневзвешенный износ колесных пар этого предприятия.

Выводы по главе

1. Подвергнуто критике уравнение показательной функции кривой возвышения продольного профиля крестовины прототипа.
2. Для описания формы возвышения продольного профиля выбрана параболическая зависимость, позволяющая, наиболее точно зеркально отобразить кривую износа поверхности крестовины.
3. Выполнен вывод уравнений кривой формы возвышения продольного профиля на основе парабол 7-й, 5-й и 3-й степени. Уравнение кривой 3-й степени, ввиду простоты вычислений, выбрано приоритетным для внедрения на производство.
4. Количественная оценка запаса металла на износ в сравнении с площадью износа показала достаточно высокую точность зеркального отображения кривой износа кривыми на основе парабол 7-й, 5-й и 3-й степени.
5. Специально для путей необщего пользования разработана методика построения поперечных профилей для крестовин с запасом металла на износ. Рекомендован уклон усовика относительно сердечника 1/9, равный средневзвешенному износу бандажей колесных пар, обращающихся на путях необщего пользования.