- Обзор методов определения напряжений и деформаций в контактной зоне рельса
- Расчёт напряжённо-деформированного состояния острякового рельса по методике Герца- Беляева- Яковлева
- О перспективах задачи расчёта контактных напряжений в элементах стрелочных переводов
- Список литературы
Цикл статей:
Глава 1 — Ресурс основных элементов стрелочных переводов типов р50 и р65 марок 1/9 и 1/11 при обращении вагонов с нагрузкой от оси 250 — 300 кн
Глава 2 — Остаточные деформации металлических элементов стрелочных переводов и их эксплуатационный ресурс
Глава 3 — Динамические испытания на путях промышленного полигона
Глава 4 — Состояние и перспективы расчёта контактной задачи «колесо-рельс»
Глава 5 — Численные методы решения контактной задачи в зонах перекатывания стрелочных переводов
Глава 6 — Применение контактных отпечатков к определению напряжённо-деформированного состояния контактной зоны конструкций с учётом пластичности и близости боковых граней элементов
Глава 7 — Определение экономической эффективности предложений по увеличению эксплуатационного ресурса
Обзор методов определения напряжений и деформаций в контактной зоне рельса
В настоящее время по всей сети магистральных железных дорог РФ происходит постепенный переход на более тяжёлый тип ВСП: по приказу МПС №12Ц от 1994 г. в основном применяются новые рельсы и переводы типа Р65, другие укладываются как старогодние. В сочетании с повышенными динамическими нагрузками на путь увеличение жёсткости приводит к интенсивному дефектообразо- ванию по причинам контактно-усталостного характера.
Контактная прочность зависит от геометрии соприкасающихся тел, расположения зон контакта, от свойств материала и состояния поверхности катания. Динамические нагрузки на элементы стрелочного перевода определяются жесткостью системы, массами и скоростями соударяемых элементов.
Особенностями стрелочного перевода являются специфические элементы зоны перекатывания с уменьшенной до 40-20 мм и менее шириной поверхности катания. При этом площадка контакта часто перекрывает поверху всё сечение.
Впервые общее решение контактной задачи для двух соприкасающихся тел с криволинейными поверхностями на основании теории потенциала получил в 1881 г. Г.Герц. Доказано распределение напряжений по поверхности контакта в виде полуэллипсоида. Позже М.Губером рассмотрен частный случай вдавливания с круговой площадкой контакта, а С.Фукс получил распределение напряжений под поверхностью контакта.
В 1913 году Г.Лоренц, а позже Л.Фешшь вывели решение контактной задачи в общем виде. С.П.Тимошенко и В.Л.Бвдерман впервые применили теорию Герца для создания простых расчётных схем решения инженерных задач [118]. Экспериментальной проверкой теории, помимо самого Герца, занимались Р.Штрибек, В.Н.Трейер, Г.Оппель.
В конце девятнадцатого века Черутти рассмотрел действие касательных сил на упругое полупространство. Б.С.Ковальский обосновал переход к плоской задаче и пропорциональность касательных и нормальных напряжений. Впоследствии А.Н.Динник рассмотрел контактную задачу с применением теории максимальных касательных напряжений, выявил распределение их и наиболее напряжённую точку на глубине, показал влияние динамики приложения нагрузки. Необходимо упомянуть работы ММСаверина [103], где дана картина напряжений для контакт цилиндра и полупространства при произвольно ориентированной касательной нагрузке.
Проблему зависимости параметров эллипса от радиусов соприкасающихся тел, распределения напряжений и их практического расчёта подробно исследовал проф.ЛИИПСа Н.М.Беляев [8,9,10]. Из более современных исследований необходимо отметить работу Й.Я.Штаермана, выявившего особенности контакта выпуклого и вогнутого тел [133], Н.И.Мусхелишвили, А.И.Лурье, М.З.Народецкого, Н. А.Кильчевского[52].
Для практических расчётов контактных напряжений большое значение имеют работы сотрудников ВНИИЖТа Шура, Порошина, Колотушкина, Тарнополь- ского [53,116] и особенно проф.ЛИИЖТа В.Ф.Яковлева, исследовавшего условия взаимодействия пути и подвижного состава и разработавшего при помощи моделей из эпоксидной смолы систему учёта приближения боковых граней, микронеровностей, близости радиусов контактных поверхностей с помощью коэффициентов к относительным деформациям [136-138]. Работы в этом направлении продолжил асп. Ж.Ж.Момбо, предложивший аналитический метод расчёта контактных напряжений при близости боковой грани на основе интегральных преобразований граничных условий плоского напряжённого состояния [71].
Для дальнейших разработок необходимо привести некоторые теоретические данные, характеризующие возможности расчёта контакта двух цилиндров.
Теория Герца-Беляева. Предпосылки:
- контактирующие тела изотропны, однородны;
- только упругие деформации по закону Тука;
- нормальное распределение давления, без трения;
- линия действия сил проходит через центр сечений;
- размеры контактных площадок сравнительно малы, поверхности идеально ровные.
а) случай первоначального касания в точке
Опасными точками по нормальным напряжениям являются центр эллипса и конец большой полуоси для вытянутого эллипса.








Расчёт напряжённо-деформированного состояния острякового рельса по методике Герца- Беляева- Яковлева
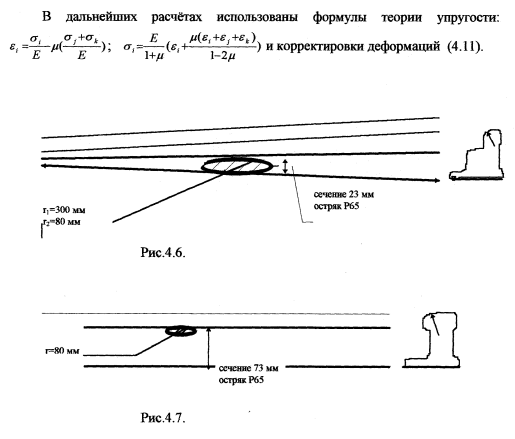
В целях оценки результатов по новым методикам приведён расчёт для контактной зоны острякового рельса при нагрузках 50; 100; 150 кН на колесо в сечениях 23 и 73 мм, где определялись контактные площадки.
Решим по теории Герца- Беляева две задачи контакта тел — с г=0,3 м на середине сечения и г=0,08 м у боковой выкружки. Применим к ним для сечения 23 мм коэффициенты малости головки, а для сечения 73 мм только во втором случае — коэффициенты близости края по методике проф.В.Ф.Яковлева.
Исходные данные: R=0,475 м — радиус колеса у вагонов, ф= 1 — расчёт при отсутствии касательных сил,
кф=1,6- средний коэффициент учёта фактической площади контакта,
//=0,3 — коэффициент Пуассона,
Е=0,21 *106 МПа — модуль упругости рельсовой стали. Параметры контактных площадок по формулам (4.1) представлены в таблице 4.1. Результаты расчётов представлены в таблицах 4.2-4.4, расчётные схемы и графики напряжений показаны на рисунках 4.6,4.7.

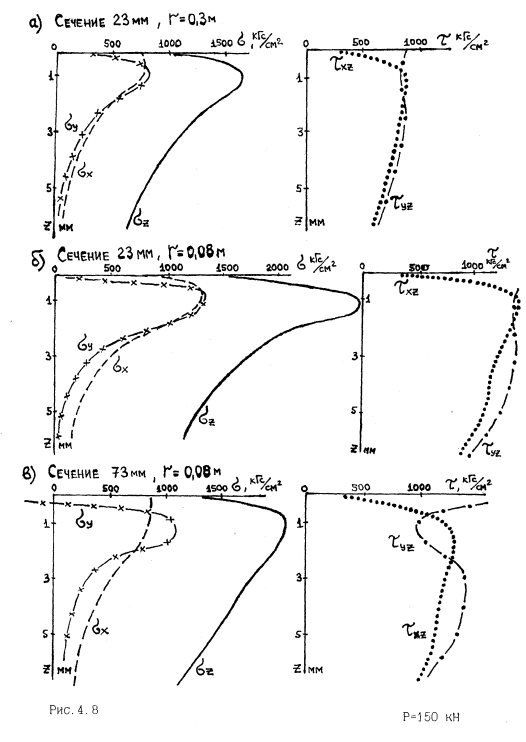
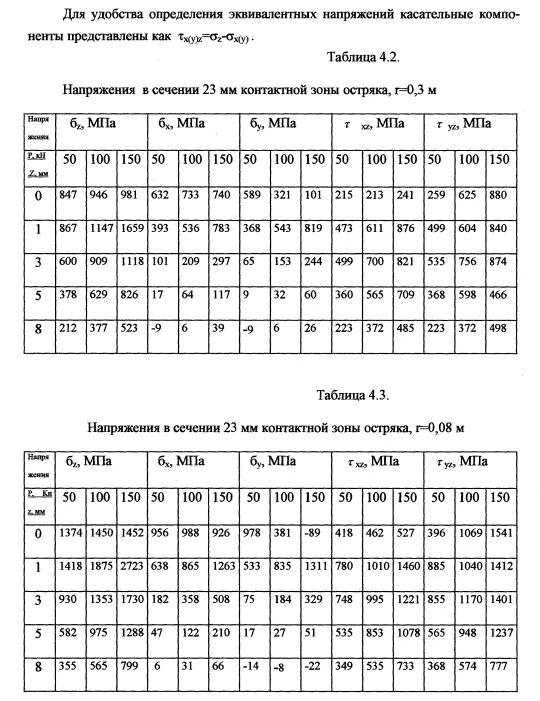
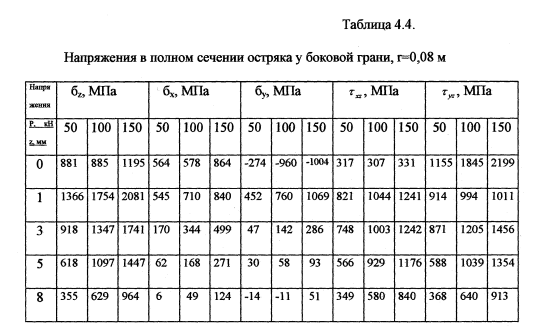
Выделяется зона на поверхности контакта при малом радиусе выкружки элемента, когда касательные напряжения достигают 1500-2200 МПа. В целом при контакте по г=0,08 м по сравнению с радиусом поверхности остряка г=0,3 м напряжения возрастают в 1,5-2 раза, а поперечная компонента меняет знак, указывая на наличие растяжения с величиной до 1000 МПа в связи со смещением металла в стороны. В случае малой ширины головки с возрастанием нагрузки наблюдается перераспределение напряжений — бу падают в 2 и более раз, т^ имеют два
максимума — один на глубине 3 мм и основной на поверхности. Причём при приближении боковой грани максимум продольных касательных напряжений увеличивается на глубине 1 мм в 1,3 раза, а поперечных — на поверхности в 3 и более раз.
Кривые 6i получили по сравнению со стандартными выпуклость на уровне z=l мм. При Р=100-150 кН глубина влияния фактора близости боковой грани достигает 10 мм. Относительные деформации по оси Z при условии упругой работы достигают 0,9 % при Р=150 кН на глубине 1 мм.
Необходимо отметить, что радиус поверхности катания г=0,3 м обеспечивает контактную прочность даже ослабленного сечения до нагрузок 150 кН/колесо, а
для г=0,08 м условие прочности нарушается в случае близости края уже при Р>50 кН. Это приводит как к смятию на 2-3 мм, так и к трещинообразованию, поэтому следует сохранять больший основной радиус поверхности катания за счёт шлифовки и закалки на глубину 10-15 мм.
Результаты этого расчёта будут в главах 5 и 6 сравниваться с данными предложенных численных и аналитических методов решения задачи и экспериментов.
О перспективах задачи расчёта контактных напряжений в элементах стрелочных переводов
В данной задаче представляется наиболее важной проблема расчёта напряжённо-деформированного состояния в случае малости размеров сечения поверху у остряка и сердечника крестовины перевода. Необходимо также исследовать влияние пластических свойств металла и учесть по возможности упругие свойства под- рельсового основания.
Для решения этих задач возможно использование следующих методов :
- адаптирования решений Митчела [126] и В.В.Соколовского [112,113] для упругого и пластического клина, загруженного равномернораспределённой нагрузкой или силой на вершине;
- конечноэлемешного анализа поперечных сечений крестовины и остряка на упругом основании с заданными на поверхности граничными условиями [105];
- экспериментальное определение контактных отпечатков под колёсной нагрузкой на реальных элементах перевода с пересчётом их параметров в напряжения и деформации и учётом пластичности металла.
В первом и особенно втором случае предусматривается применение ПЭВМ. Указанные исследования необходимы также для выявления особенностей напряженно-деформированного состояния, прогнозирования дефекгообразования и выработки рекомендаций по улучшению конструкций. Установление связей между нагрузками, геометрией элементов и контактно-усталостными дефектами представляет одну из основных проблем транспорта, решение которой способно принести значительный экономический эффект.
Список литературы
- Мелентьев Л.П., Вахненко В.И. Осевые нагрузки и сроки службы рельсов// Путь и путевое хозяйство,-1981.- N 7.- с. 9.
- Мелентьев Л.П. Особенности работы рельсов в тяжёлых условиях эксплуатации // Рельсы повышенной прочности для особо тяжёлых условий эксплуатации: Сб. науч. тр. ВНИИЖТа. —
М.: ТранспортД970,- Вып.428,- с. 21-24. - Мелентьев Л.П. О форме контактной поверхности пары «колесо — рельс» // Вестник ВНИИЖТа.- 1983,- N 5,- с. 11.
- Митягин Ю.И. О допустимых контактных нагрузках на рельсы // Изучение напряжённого и деформированного состояния пути и стрелочных переводов: Сб. науч. тр. ЛИИЖТа; Под ред. В.Ф Яковлева.- Л.,1969,- Вып.296,- с. 62-68.
- Михайлова В.П., Путря H.H. Эффективность улучшения качества металла крестовин типа общей отливки// Сб. науч. тр. ВНИИЖТа; Под ред. Н.Н.Путри.- М.Транспорт, 1988.- с. 78-85.
- Михалёв М.С., Путря H.H., Кац Р.З. Причины образования и пути ликвидации дефектов контактной усталости литой части крес¬товин // Тр. ЦНИИ МПС,- М.:Транспорт,1971.- Вып.431,- с. 35-37.
- Момбо Ж.Ж. Разработка метода расчёта контактных напряжений в зоне боковой выкружки головки рельса: Дис….канд. тех. наук: 05.22.06. — Защищена в 1989 г в ЛИИЖТе.- Л.,1989.-126 е.- Библиогр. с. 117-125.
- Нагрузки, скорости, грузонапряжённости, путь /Г.М.Шахунянц и др.//Вопросы пути и путевого хозяйства: Сб. науч. тр. МИИТа.- М.,1973.- Вып.443,- с. 4-7.
- Наибольшие допустимые величины износа основных металличес¬ких частей стрелочных переводов путей МПС. Доп. к РТМ.32/ЦП-3-75, утв. приказом N М-2460 от 27.07.80. — М.,1980.
- Наплавка крестовин в магнитном поле // Путь и путевое хо¬зяйство,- 1983.- N 10.- с. 22.
- Наркевич В.В. Совершенствование геометрических параметров крестовин типа общей отливки // Сб. науч. тр. ВНИИЖТа; Под ред. Н.Н.Путри.- М.Транспорт, 1988,- с. 70-77.
- На участках обращения вагонов с высокими осевыми нагрузками (Австралия) // Путь и путевое хозяйство.- 1982.- N 5.- с. 12.
- Никонов А.М., Артамонов В.А. Распределение пластической де¬формации в зоне поверхности катания головок рельсов // Исс¬ледование работы скреплений и рельсов: Сб. науч. тр. МИИТа; Под ред. Г.М.Шахунянца.- М.,1971.- Вып.354- с.104-108.
- Никонов А.М. Изменение профиля головки рельсов при высоких нагрузках // Повышение уровня использования и надёжности ра¬боты железнодорожного пути: Сб. науч. тр. МИИТа.- М.,1988.- Вып.796.- с. 7-10.
- Нормы допускаемых скоростей движения локомотивов и вагонов по железнодорожным путям и стрелочным переводам колеи 1520 мм: Приказ МПС N 8ЦЗ.- М.Д979.
- Нормы допускаемых скоростей движения по стрелочным переводам колеи 1520 мм; Приказ МПС N 1531 от 15.04.85.- М.,1985.