Оценка влияния сварки стыков в стрелочных переводах на взаимодействие пути и подвижного состава

• Постановка вопроса
• Моделирование взаимодействия подвижного состава и пути взоне одиночного рельсового стыка
• Моделирование взаимодействия колес подвижного состава и элементов стрелочного перевода
• Оценка напряжений в зоне рельсового стыка до и после сварки стыка
• Экономическая эффективность алюмо-термитной сварки стыков стрелочного перевода
• Выводы
• Список литературы

Моделирование взаимодействия подвижного состава и пути в
зоне одиночного рельсового стыка

Для оценки влияния зазора и динамической ступеньки на величины действующих в динамике сил рассмотрим взаимодействие подвижного состава и пути в зоне рельсового стыка с использованием модели, разработанной профессором Э.П.Исаенко и к.т.н. М.В.Безруковым [69], приведенной на рис.65. В связи с широкой укладкой на перегонах и станциях бесстыковых плетей вперемешку со старыми путями и стрелочными переводами на дереве возникли три характерных схемы взаимодействия колеса и рельса в стыках: колесо перекатывается с пути на железобетонных шпалах на такой же путь на железобетонных шпалах, колесо перекатывается с пути на деревянных шпалах на путь с железобетонными шпалами и наоборот, колесо перекатывается с пути на деревянных шпалах на путь на деревянных шпалах. В перспективе на магистральных железных дорогах МПС РФ должна остаться первая схема, а стыки должны быть сварены для создания условий обеспечения плавного и безударного качения колеса.

Исходные данные для выполненных далее динамических расчетов приведены в таблице 9.

Рассмотрим силе взаимодействия колеса пассажирского вагона и рельсов при прохождении вагоном рельсовых стыков. Модель для оценки динамики вертикальных и продольных сил в стыке [69] приведена на рис.65.

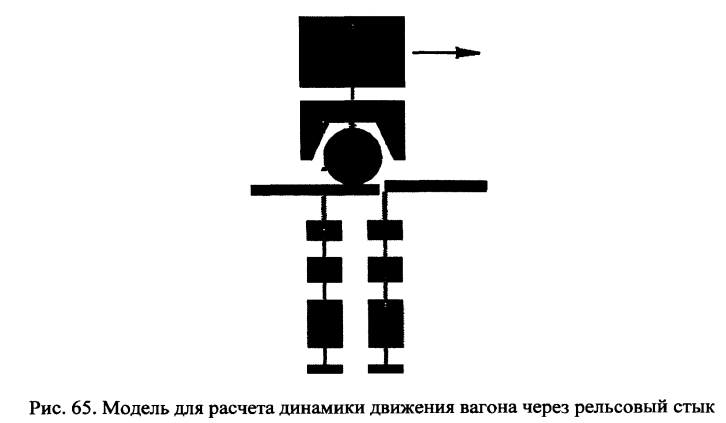
В приведенной на рис.65 модели основание насыпи принято абсолютно жестким, что исключает влияние его податливости. В модели учтены характеристики рессорного подвешивания вагона (упругость и демпфирование) и упругие и демпфирующие характеристики пути. Начальные величины зазоров в стыках могут принимать различные значения, далее во всех расчетах максимальный зазор принят равным 35мм. Уменьшение величины зазора в стыке приводит к уменьшению величины продольной силы в принимающем конце рельса. Начальная статическая ступенька в стыках принята не превышающей 1мм (принимающий конец рельса выше отдающего). Динамическая ступенька зависит от сил воздействия колес на принимающий и отдающий рельсы и определяется во время расчета модели. Величины этих сил и динамической ступеньки зависят от скорости движения вагона, сочетания амплитуд и фаз колебаний системы.

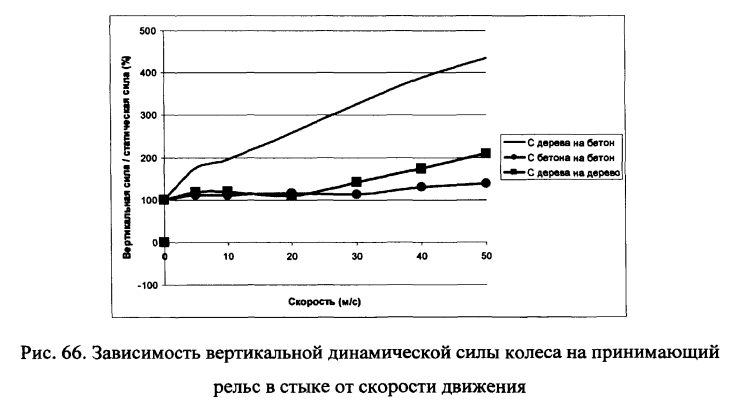
Результаты выполненных динамических расчетов — зависимости динамических характеристик взаимодействия от скорости вагона приведены на рис.66-67. Как видно из сравнения рис.66-67 наихудшая ситуация возникает при перекатывании колеса с пути на деревянных шпалах на путь с железобетонными шпалами — например въезд со звеньевого пути на бесстыковую плеть на железобетоне. В этом случае при скорости движения 50м/с вертикальная сила в стыке достигает почти 500% от статической. Наименьшее значение вертикальная сила имеет при перекатывании колеса с пути на железобетонных шпалах на путь с железобетонными шпалами — вертикальная сила при той же скорости достигает 150% от статической нагрузки). При перекатывании «с дерева на дерево» она больше и достигает 200% статической. Увеличение сил при перекатывании «с дерева на дерево» вызвано большей вертикальной деформативностью деревянных шпал по сравнению с железобетонными и увеличением из-за этого «динамической ступеньки».

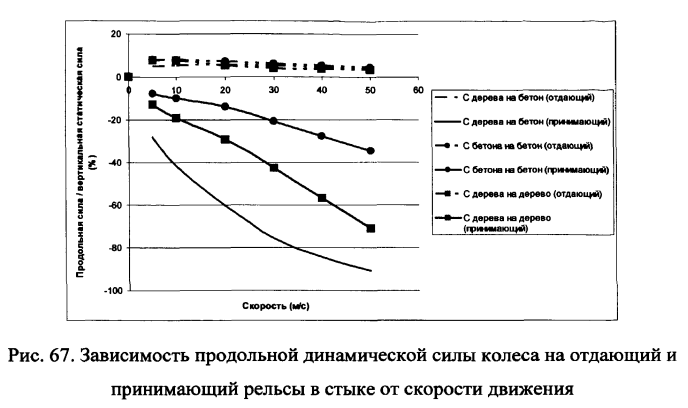
Оценки сил продольного удара в стыке на принимающий и отдающий концы рельсов показаны на рис.67. Как и на рис.66 худшая ситуация возникает при перекатывании колеса «с дерева на бетон» (до 90% от статической нагрузки при статической ступеньке не более 1мм) и лучшая при перекатывании «с бетона на бетон» (до 35% от статической нагрузки).

Перекатывание колеса через рельсовый стык вызывает в рельсах более сложное напряженное состояние и более высокие напряжения из-за больших значений вертикальных и продольных сил, чем при качении колеса по бесстыковому пути.

Моделирование взаимодействия колес подвижного состава и элементов стрелочного перевода

Движение вагона по стрелочному переводу с не сваренными рельсовыми стыками приводит к усилению колебаний вагона, при этом колесо к стыку может подходить в разных фазах колебаний (нагрузка-разгрузка) и нагрузка на рельс может возрастать и спадать в зависимости от скорости движения вагона и предыстории колебаний вагона перед переводом.

Взаимодействие колеса и рельсов в стыке зависит от предыстории движения. Практический интерес представляет рассмотрение движения вагона через стрелочный перевод в прямом направлении (рамные рельсы, рельс перед крестовиной и остряк, крестовина, рельсы за крестовиной) — колесная пара будет подходить к этим стыкам в разных фазах колебаний.

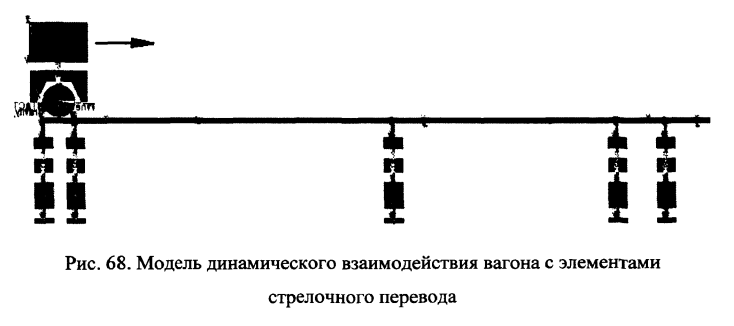
Модель расположения стыков на стрелочном переводе приведена на рис.68. В модели приняты следующие расстояния между стыками:

-от первого стыка до второго — Юм,

-от второго стыка до третьего 7м, третий стык — крестовина стрелочного перевода.

-от крестовины до стыка в хвосте крестовины — 1.5м,

-от четвертого стыка до пятого стыка — 10м.

На рис.69-80 показаны рассчитанные динамические вертикальные силы взаимодействия колеса вагона с рельсовыми нитями и отдельными элементами стрелочного перевода при различных скоростях движения. На рис.81 для сравнения эти графики нанесены одновременно.

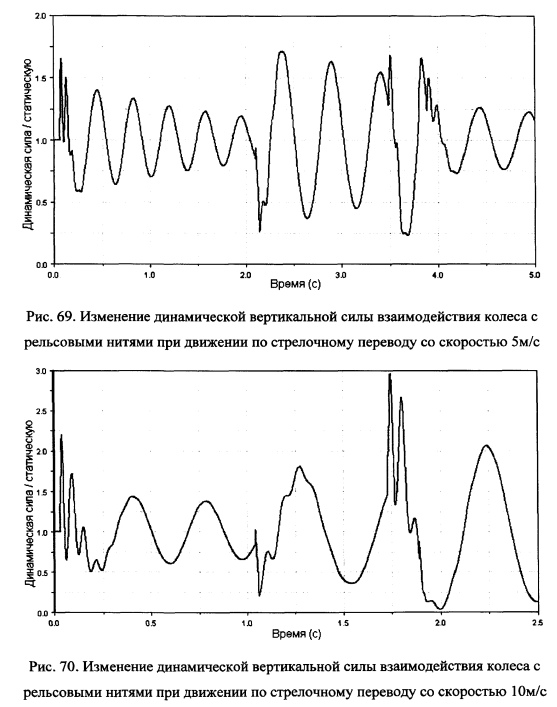
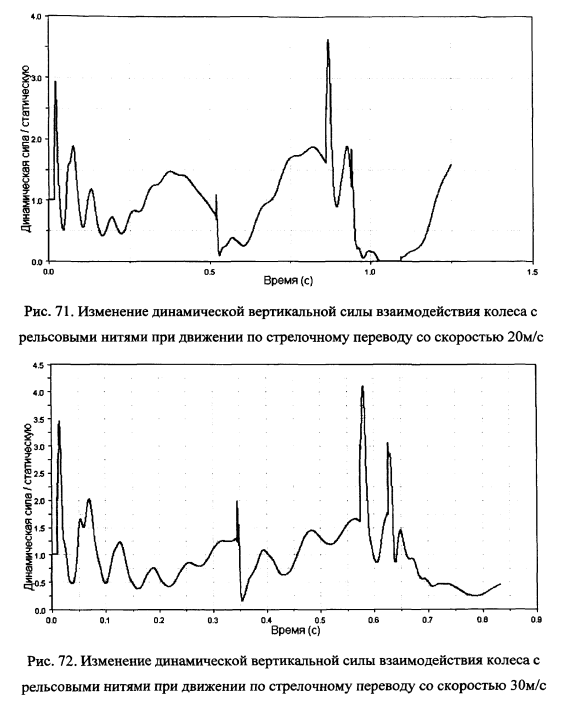
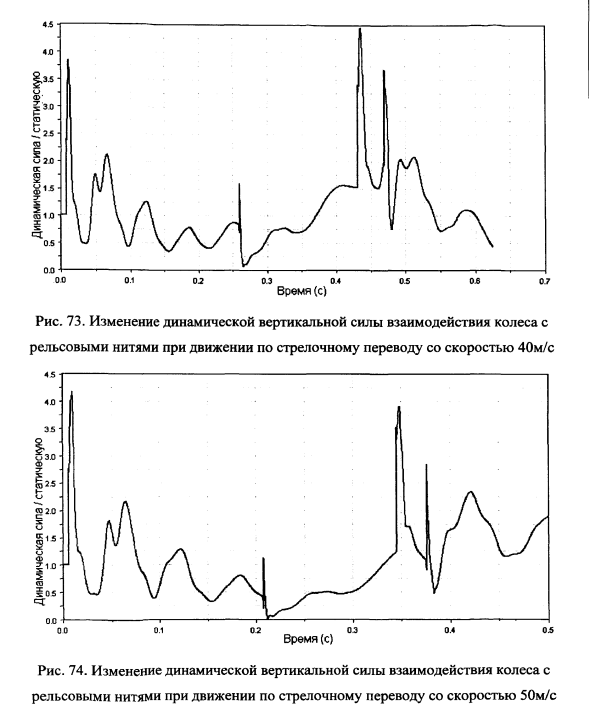
Как видно из сравнения приведенных выше графиков при прохождении стыков сила взаимодействия колеса и рельсовых нитей меняется в зависимости от фазы колебания элементов вагона и пути. Возможны как полная разгрузка колеса, так и возрастание нагрузки в 4-5 раз по сравнению со статической, что существенно превышает значение коэффициента динамики при движении вагона по рельсовой колее с отступлениями 1-ой степени равное 1.3-1.6.

Изменение динамической вертикальной силы, действующей на части стрелочного перевода показано на рис.75-80.

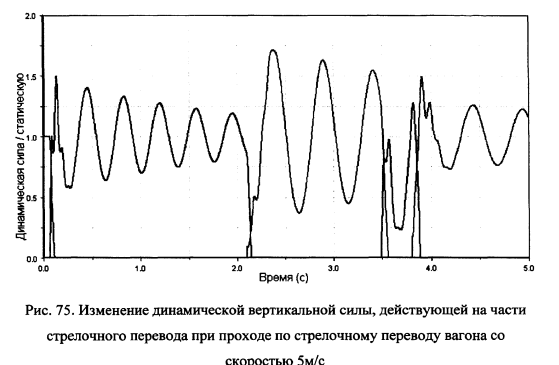
Как видно из сравнения графиков, приведенных на рис.75, не смотря на то, что колесо подходит к первому рельсу «уравновешенным» — его давление на рельс равно статическому, при скорости 5м/с уже в первом стыке формируется максимум вертикальной силы, составляющий 150% от статической нагрузки. При перекатывании на второй рельс колесо имеет две точки опоры (на первый и второй рельсы). Далее происходит затухание амплитуды колебаний. Вертикальная динамическая сила на второй рельс больше, чем на первый. При данной скорости в стыке перед крестовиной и при перекатывании через «мертвое пространство» крестовины вертикальная нагрузка оказалась меньше, чем во втором стыке.

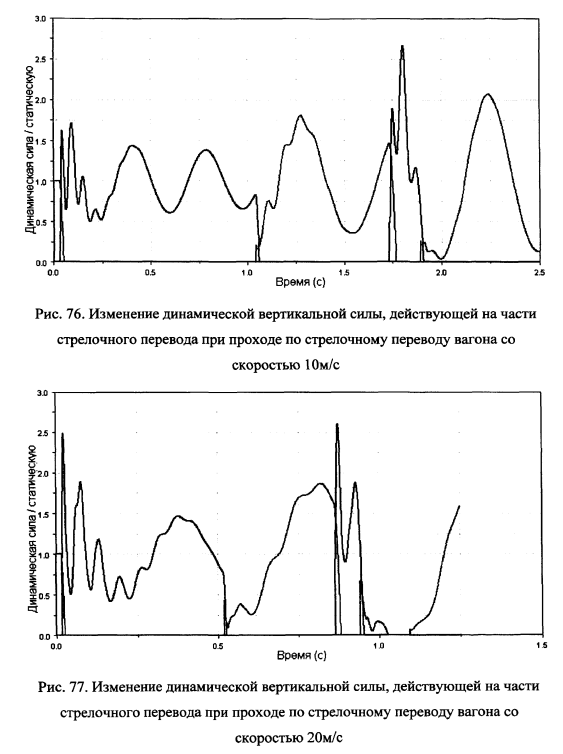
Уже при скорости 10м/с, как показано на рис.76, вертикальная нагрузка при перекатывании колеса через зазор в крестовине больше, чем в во втором стыке, где она упало почти до нуля. Как видно из графиков вертикальных нагрузок на элементы стрелочного перевода, приведенные на рис.77, после перекатывания колеса через крестовину со скоростью 20м/с наблюдается участок отрывного качения колеса по рельсу (вертикальная сила взаимодействия колеса с рельсом равна 0 в течении определенного интервала времени) — колесо «прыгнуло» над поверхностью рельса.

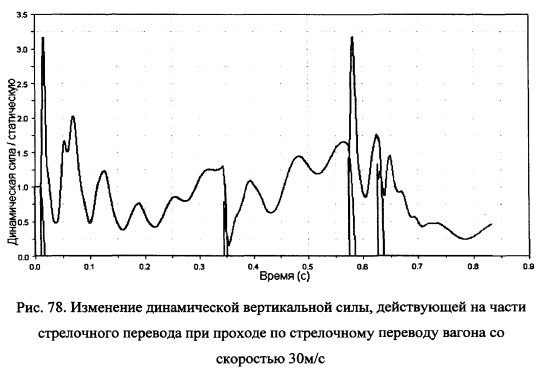
При скорости 30м/с отрывного качения не произошло, а вертикальный удар в крестовину составил по величине 3.2 от статической нагрузки (рис.78).

При скорости 40м/с наблюдается рост вертикальной нагрузки до 3.7 от статической (рис.79). На втором стыке происходит почти полная разгрузка колеса.

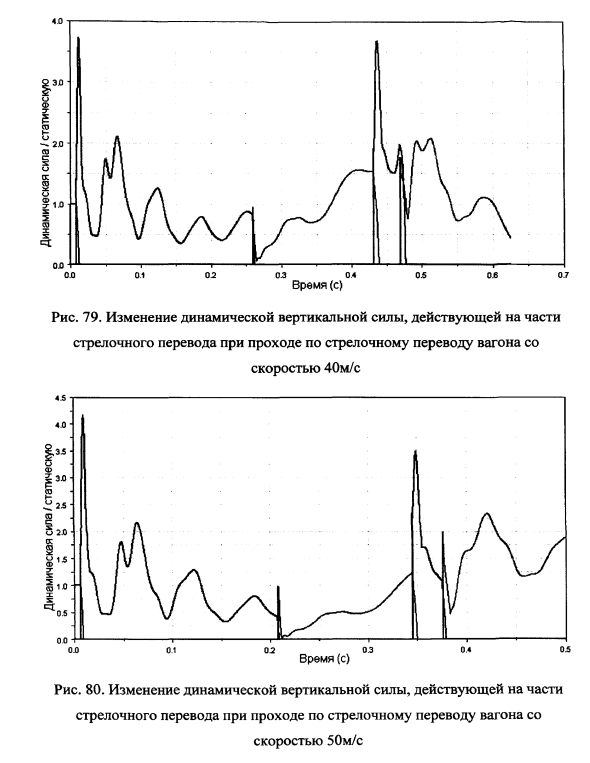
При скорости вагона 50м/с максимум вертикальной силы наблюдается уже в первом стыке (рис.80) и достигает 4.2 от статической нагрузки.

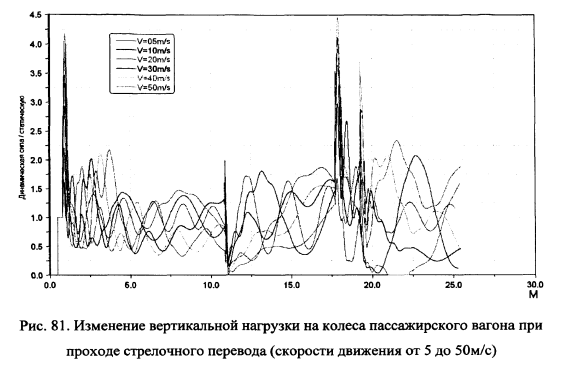
Как видно из сравнения графиков рис.81 вертикальная нагрузка на элементы
стрелочного перевода меняется в широком диапазоне значений, который
определяется как скоростью движения, так и фазой колебаний вагона, которая в
свою очередь является «случайной» величиной, в том смысле, что ее нельзя
заранее определить — она определяется предысторией колебаний вагона на
неровностях пути и стыках. Средний уровень максимальных динамических
нагрузок на элементы стрелочного перевода со стыками примерно в два раза
выше, чем на средней части плети бесстыкового пути. Максимальные значения
вертикальной нагрузки на рельсы и колеса вагона превышают вертикальные
нагрузки на бесстыковом пути в 3.5-4.5 раз при скоростях более 40м/с. Этим и
определяется меньший ресурс элементов стрелочного перевода в сравнении с
ресурсом рельсов бесстыковых плетей.

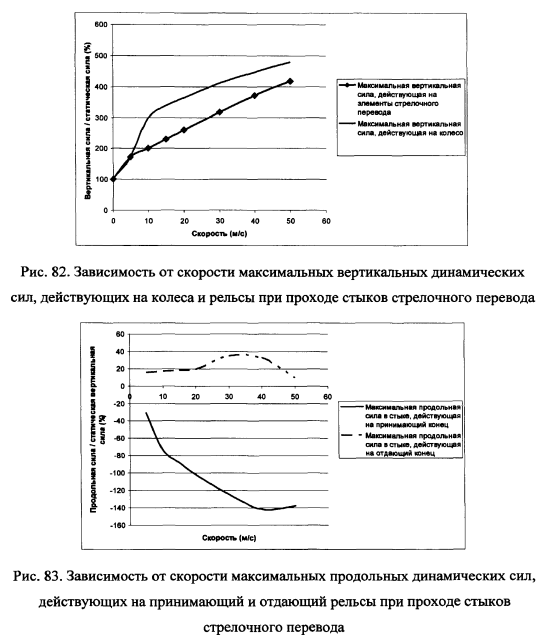
На рис.82-83 приведены огибающие максимальных вертикальных и продольных сил в стыках при проходе стрелочного перевода.

Из сравнения данных приведенных выше графиков можно сделать вывод, что при любой скорости движения прохождение колесом первого стыка приводит к резкому усилению вертикальной нагрузки на рельс. В диапазоне скоростей движения 5-50м/с не удается избежать пика вертикальной силы при проходе крестовины. В указанных местах вертикальная нагрузка колеса на рельс возрастает на 200-300%, что существенно снижает ресурс рельсов, элементов стрелочного перевода и колес.

Для повышения ресурса стрелочного перевода и колес вагонов необходимо выполнить сварку всех рельсовых стыков, проводить мероприятия, повышающие срок службы крестовины и ее устойчивость к вертикальному и боковому износу.

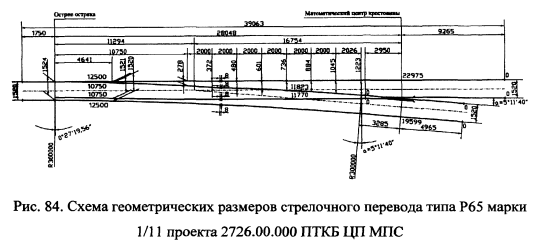
Наиболее целесообразным решением является укладка на скоростных участках стрелочных переводов с непрерывной поверхностью катания по крестовине (например — перевод проекта 2726.00.000 ПТКБ ЦП МПС типа Р65 марки 1/11 Муромского стрелочного завода). Крестовина с непрерывной поверхностью катания, с гибко-поворотным сердечником создает непрерывность рельсовой колеи, что позволяет обеспечить по прямому направлению скорости движения до 180км/ч (после сварки стыков). Конструкция перевода проекта 2726 предусматривает длину рамного рельса равного 16.08м, гибкий остряк длиной 10.75м, применение упругих клеммы.

Использование на скоростных участках пути стрелочных переводов типа Р65 марки 1/11 проекта ПТКБ ЦП МПС 2750.00.000, в которых применены гибкие остряки на подкладках с высокими ребордами, упругое скрепление рамных рельсов, крестовина сварной конструкции с увеличенным задним вылетом имеет значительные преимущества перед другими типами стрелочных переводов. Но в этом переводе есть разрыв колеи в крестовине, которая будет подвергаться усиленному износу из-за больших динамических нагрузок. При эксплуатации таких переводов необходимы меры против износа крестовины, применение специальных смазок, создающих тонкую и прочную пленку масла на поверхности металла, которая долго сохраняется на поверхности катания.

Оценка напряжений в зоне рельсового стыка до и после сварки стыка

Выполним расчет контактных напряжений в рельсах до и после сварки стыков для полученных выше при скорости движения более 40м/с величин действующих сил от подвижного состава. Используем конечно-элементные модели сваренного алюмотермитным способом рельсового стыка (рис.85) и стыка, в котором рельсы соединены двухголовыми стыковыми накладками с зазором 10мм. Вертикальная нагрузка колеса на бесстыковый рельс составляет Юте, вертикальная нагрузка на рельсовый стык 13тс и продольная сила на принимающий торец рельса 3.2тс, на отдающий конец рельса 0.4тс.

Расчеты выполнены с использованием программного комплекса COSMOS/M. Конечно-элементная модель обычного рельсового стыка, соединенного стыковыми накладками, состоит из 58000 элементов типа Solid. Модель сваренного алюмотермитным способом рельса состоит из 42000 элементов того же типа.

Сравнение напряженно-деформированного состояния металла головки рельса в этих двух моделях выполним по критерию Мизеса,

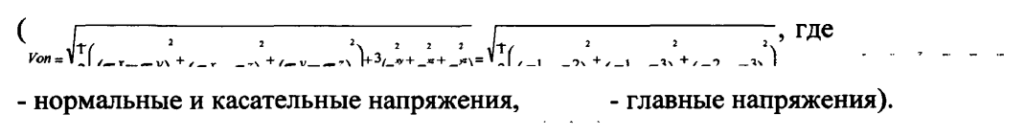
Критерий Мизеса определяется величинами главных, нормальных и касательных напряжений при объемно-напряженном состоянии рельса — чем выше значения критерия Мизеса, тем больше вероятность разрушения материала.

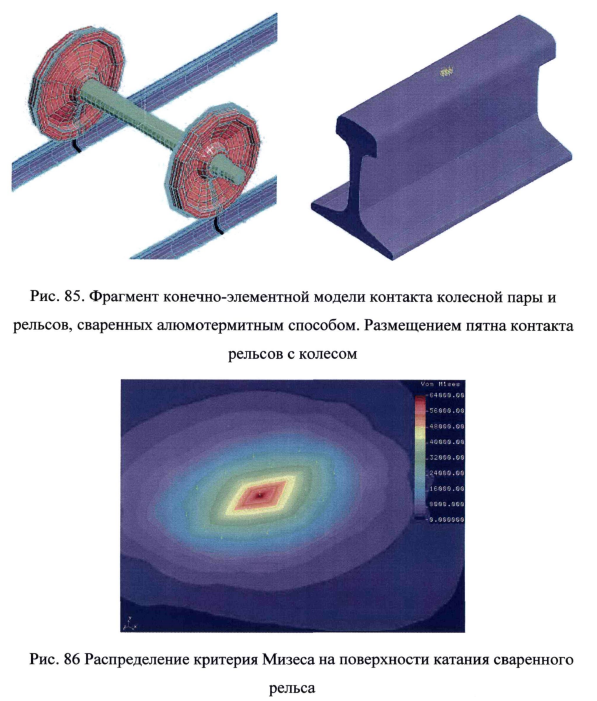
Расчетное пятно контакта имеет форму близкую к эллипсу, а максимальные
контактные значения критерия Мизеса достигают б000 кгс/см 2 . Максимальные
вертикальные напряжения сжатия близки к 5000 кгс/см 2.

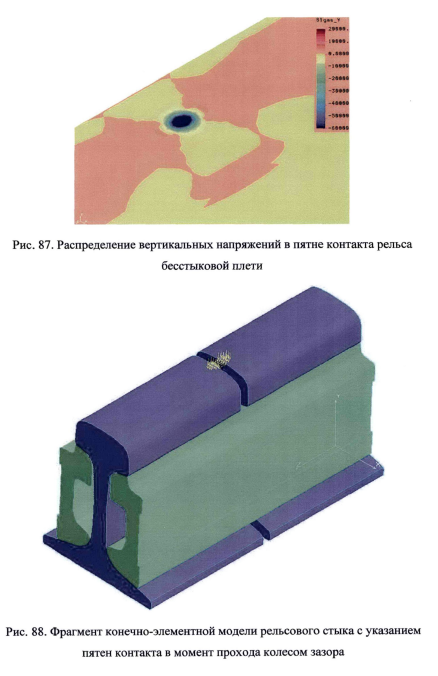
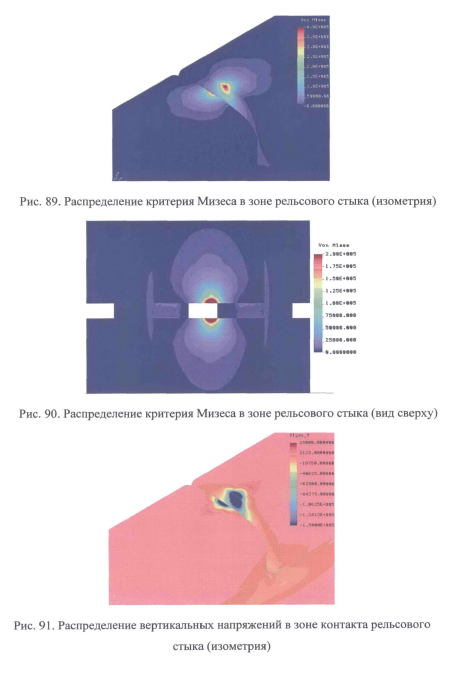
Расчетные напряжения в отдающем и принимающем торцах рельсов существенно отличаются по величине.

Разница в распределении напряжений от воздействия подвижного состава в двух рассмотренных случаях очень велика. Для случая прохождения колесом стыка численные значения критерия Мизеса в головке рельса в три-четыре раза больше, чем при прохождении средней части рельсовой плети. Вертикальные контактные напряжения в рельсах бесстыковой плети в два-три раза меньше, чем при прохождении рельсового стыка. В рельсах стыка контактные напряжения достигают предела текучести и здесь часто происходят пластические деформации, формируются дефекты первой и пятой групп, повышается износ рельсов.

Из-за увеличения напряжений в рельсах в два-три раза срок службы снижается примерно в 10 раз. Так, если рельс в средней части плети может наработать до 1500млн.т.брутто, то в зоне стыка наработка составит примерно 150млн.т.брутто. Особенно невыгодно иметь стыки на стрелочных переводах, которые стоят очень дорого, а из-за наличия в стрелочных переводах рельсовых стыков их срок службы сокращается в два-три раза (плановая наработка рельсов в стрелочных переводах составляет 350млн.т.брутто, а фактическая при наличии рельсовых стыков по оценкам ВНИИЖТ составляет 120-130млн.т.брутто). Технология алюмо-термитной сварки рельсовых стыков достаточно апробирована на железных дорогах МПС РФ.

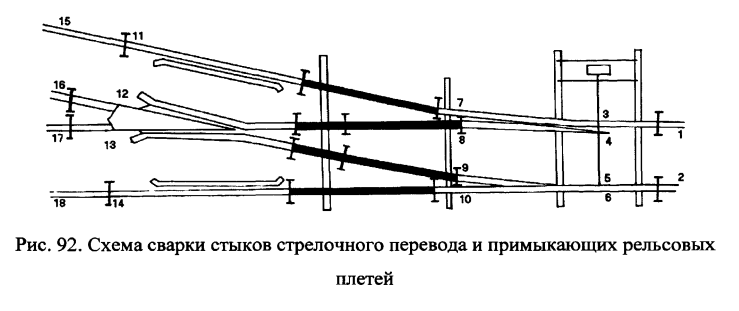
В 1997г на станции Ильино при участии сотрудников ВНИИЖТ выполнена
сварка стыков стрелочного перевода №14. После сварки стыков стыковые
накладки были сохранены и возвращены на прежнее место после фрезеровки в
средней части для размещения части металла сварного стыка, который остается после срезки грата (рис.93-94). В течение пяти лет после сварки все сваренные стыки работают без замечаний, износ элементов стрелочного перевода уменьшился. После сварки стыков работа стрелочного перевода стала стабильнее, а темпы накопления осадок балласта резко снизились. Горьковская железная дорога приняла решение о сварке рельсовых стыков в пределах стрелочных переводов, что обеспечивает сокращение эксплуатационных расходов на содержание подвижного состава и элементов пути.

Экономическая эффективность алюмо-термитной сварки стыков стрелочного перевода

Стоимость алюмо-термитной сварки одного рельсового стыка в настоящее время близка к 100$ США. Всего на стрелочном переводе в прямом направлении приходится сваривать 6 стыков и 4 стыка на боковое направление. Цена сварки стыков одного стрелочного перевода близка к 1000$ США.

Расчетная наработка стрелочного перевода типа Р65 марки 1/11 проектов 2726 и 2750 на железобетонных брусьях с рельсовыми стыкам по данным ВНИИЖТ принята 130млн.т.брутто. При условии сварки стыков расчетная наработка соответствует паспортной и равна 350млн.т.брутто.

Стрелочный перевод типа Р65 марки 1/11 проекта 2726 стоит 420тыс.руб. Стрелочный перевод типа Р65 марки 1/11 проекта 2750 без железнодорожного тарифа и без рельсовых замыкателей стоит 400тыс.руб. Ежегодные расходы на эксплуатацию стрелочных переводов без сварки стыков и наработке за год 40млн.т.брутто составляют: стрелочный перевод проекта 2726 — 41.0тыс.руб., стрелочный перевод проекта 2750 — 58.3тыс руб.

После сварки стыков при наработке за год 40млн.т.брутто ежегодные эксплуатационные расходы составляют: стрелочный перевод проекта 2726 — 20.5тыс.руб., стрелочный перевод проекта 2750 — 39.0тыс.руб.

При наработке за год в 40млн.т.брутто расчетный срок службы стрелочных переводов на железобетонных брусьях без сварки стыков составит 3 года, а при сварке стыков — 9 лет. Период сравнения вариантов со сваркой стыков и без сварки стыков составит 9 лет. Рассмотрим накопление приведенных затрат по вариантам укладки на скоростных участках стрелочных переводов проекта 2726 и 2750 без сварки стыков и со сваркой стыков. Приведенные расходы определяются суммированием начальных и ежегодных затрат по вариантам с учетом коэффициента приведения. Норма эффективности капиталовложений принята равной 0.12, расчетный срок окупаемости капиталовложений — 8 лет.

Суммарные сравнительные приведенные затраты по вариантам за 9 лет эксплуатации составили:

1. Вариант      стрелочного перевода проекта 2726 без сварки стыков 924.8тыс.руб.
2. Вариант  стрелочного перевода проекта 2750 без сварки стыков ЮЮ.бтыс.руб.
3. Вариант      стрелочного перевода проекта 2726 со сваркой стыков 520.5тыс.руб.
4. Вариант      стрелочного перевода проекта 2750 со сваркой стыков 605.0тыс.руб.

Лучшим (с минимальными приведенными суммарными затратами) является вариант со сваркой стыков в стрелочном переводе проекта 2726.

Анализ полученных результатов убеждает в высокой экономической эффективности сварки стыков стрелочных переводов на участках со скоростным пассажирским движением. При грузонапряженности 40млн.т.брутто расходы на сварку стыков стрелочных переводов окупаются менее чем за один год эксплуатации без учета экономии затрат на эксплуатацию и приобретение подвижного состава. Сварка стыков стрелочных переводов на железобетонных брусьях является важным направлением экономии эксплуатационных расходов железной дороги.

Выводы

Анализ результатов расчетов и наблюдений нестационарного напряженно- деформированного состояния рельсов в зоне стыка показал, что фактически вертикальная нагрузка в стыке поочередно почти полностью воспринимается сначала отдающим, а затем принимающим рельсом. Стыковые накладки допускают относительные вертикальные перемещение концов рельсов в стыке «динамической ступеньки» также из-за допусков при изготовлении стыковых накладок и недостаточной затяжки стыковых болтов. Пятно контакта колеса в стыке имеет в 2-3 раза меньшие геометрические размеры, чем при опоре колеса на рельс плети. Анализ результатов выполненных в диссертации расчетов показал, что контактные напряжения в стыке в 3-4 раза выше, чем у рельса бесстыковой плети.

2. Установлено, что вертикальная нагрузка колеса на рельсы в стыках меняется квазислучайным образом и зависит от фазы колебаний вагона (нагрузка- разгрузка). При этом худшим является случай стыка пути на деревянных шпалах и пути на железобетонных шпалах (переход «с дерева на бетон»). Получены оценки огибающих максимальных нагрузок на рельсы и колесо при прохождении рельсового стыка. В стыке при скорости 50м/с вертикальная нагрузка на колесо может превышать статическую нагрузку в 5 раз, а на рельсы в 4.6 раза при схеме перекатывания «с дерева на бетон».
3. Установлено, что в стрелочных переводах обычно максимальные нагрузки от колес на рельсы относятся к первому стыку плети и рамных рельсов и к месту разрыва колеи в «мертвом пространстве» крестовины стрелочного перевода. Здесь при скорости движения 50м/с вертикальные нагрузки могут превысить статическую в 4-5 раз. Во избежание появления таких максимумов вертикальной нагрузки рекомендуется для скоростного движения использовать стрелочные переводы проекта 2726 с подвижным сердечником крестовины, обеспечивающим непрерывность поверхности катания колеса по крестовине. Руководством Горьковской железной дороги принято решение в дальнейшем на скоростных участках пути укладывать стрелочные переводы типа Р65 марки 1/11 проекта 2726.
4. Установлено, что из-за опоры колеса вагона на два рельса при проходе рельсового стыка на колеса вагонов действует большая нагрузка, чем на каждый из стыкуемых рельсов. Получена нелинейная огибающая максимальных вертикальных давлений на колесо вагона, зависящая от скорости движения вагона по стрелочному переводу с рельсовыми стыками.
5. Анализ результатов расчетов напряженно-деформированного состояния головки стыкуемых накладками рельсов с использованием программного комплекса COSMOS/M показал, что при скоростном движении в стыке формируются в три-четыре раза большие, чем в средней части рельсовой плети значения критерия Мизеса, а напряжения сжатия в два-три раза выше, чем в средней части плети. Наличие стыков приводит к уменьшению ресурса рельсов примерно в 10 раз и резко сокращает срок службы стрелочных переводов снижая наработку стрелочных переводов с плановых 350млн.т.брутто до 120-130млн.т брутто.
6. На основе анализа результатов выполненных в диссертации прочностных и технико-экономических расчетов руководством Горьковской железной дороги решено выполнять алюмо-термитную сварку стыков стрелочных переводов на всех скоростных участках пути, так как это обеспечит ресурсосбережение ходовых частей подвижного состава и элементов железнодорожного пути.

Список литературы

1. Прокудин И.В. Колебания глинистых грунтов земляного полотна при высокоскоростном движении поездов // Вопросы земляного полотна и геотехники на железнодорожном транспорте. Межвузовский сборник научных трудов. Выпуск 203/28. Днепропетровск, 1979, с.43-51.
2. Путь и безопасность движения поездов / В.И.Болотин, В.А.Лаптев, В.С.Лысюк, В.Я.Шульга: Под. Ред. В.Я.Шульга. Москва, Транспорт, 1994.
3. Рабчук С.А. Задачи и программа перевооружения путевого хозяйства. Путь и путевое хозяйство. 1995. №4, с.5-12.
4. Ромен Ю.С. О движении экипажей в кривых участках пути./Вестник ВНИИЖТ, 1964. №6, с. 16-20.
5. Синицин А.П. Метод конечных элементов в динамике сооружений. Москва, Стройиздат, 1978. 230с.
6. Соловьев Н.В., Новакович В.И. Резервы повышения эффективности применения машин тяжелого типа на бесстыковом пути // Тр. ВНИИЖТ, 1976, вып.554.
7. Стрельцов A.C. Применение рельсовых плетей на больших металлических мостах. Москва, ВНИИЖТ, 1994.
8. Строительная механика. Динамика и устойчивость сооружений / Смирнов А.Ф., Александров A.B., Лащенников Б.Я., Шапошников H.H. Под ред. Смирнова А.Ф. Москва, Строиздат, 1984. 416с.
9. Технические указания по устройству, укладке и содержанию бесстыкового пути. МПС РФ, Главное управление пути. Москва, Транспорт, 1992, 72с.
10. Управление техническим состоянием пути./Н.И.Карпущенко, В.А.Грищенко, Г.К.Щепотин и др. Нолвосибирск, изд. СГАПС, 1995, 205с.
11. Фадеев А.Б. Метод конечных элементов в геомеханике. Москва, Недра, 1987. 221с.
12. Хвостик М.Ю. Повышение работоспособности болтовых соединений стрелочных переводов. Москва, ВНИИЖТ, 1994.
13. Цейтлин А.И. Прикладные методы решения краевых задач строительной механики. Москва, Стройиздат, 1984. 174с.
14. Чернышев М.А. Практические методы расчета пути. Москва, Транспорт, 1967. 235с.
15. Шайдуллин Ш.Н., Исаенко Э.П., Иванов С.Ю., Безруков М.В. Влияние параметров элементов верхнего строения пути на их колебания при проходе подвижного состава // Сборник трудов 2-ой конференции CAD-FEM, Москва,.2002. Стр. 140-142.