- Краткий обзор теории механических колебаний
- Факторы, учитываемые в модели взаимодействия экипажа и пути в программной системе АОАМ8/КаИ
- Расчет собственных форм и частот колебаний пассажирских вагонов
- Расчет воздействий на путь колес пассажирских вагонов при прохождении ими системы вертикальных периодических неровностей (просадок пути)
- Движение вагона через изолированную неровность
- Движение колес вагона в кривых
- Движение вагона при периодически изменяющейся ширине колеи в прямой
- Влияние перекосов пути на вертикальные давления колес на рельсы
- Влияние амплитуды перекоса на величины максимальной и минимальной динамической силы взаимодействия колеса и рельса
- Выводы
- Список литературы
Цикл статей:
Глава 1 — Подготовка железнодорожного пути к скоростному пассажирскому движению на Горьковской железной дороге
Глава 2 — Моделирование взаимодействия пути и подвижного состава при скоростном движении пассажирских поездов
Глава 3 — Оценка влияния сварки стыков в стрелочных переводах на взаимодействие пути и подвижного состава
Глава 4 — Экспериментальные исследования работы клемм ОП-511 на анкерных участках пути
Вибрации элементов железнодорожного пути обусловлены большими силами взаимодействия между колесами и рельсами. В зависимости от неровностей колеса и рельса и конструктивных особенностей пути и подвижного состава эти силы изменяются в широком диапазоне.
Взаимодействие пути и подвижного состава изучали многие отечественные и зарубежные специалисты. В последние годы опубликовали результаты исследований этой проблемы профессора М.Ф.Вериго, С.В.Вершинский, В.А.Грищенко В.Н.Данилов, М.П.Ершков, Г.Н.Жинкин, Э.П.Исаенко Н.И.Карпущенко, С.И.Клинов, А.Я.Коган, И.В.Прокудин, И.И.Челноков, Эсвельд и многие другие. В этой проблеме недостаточно изучен вопрос об особенностях колебаний пассажирских вагонов нового поколения при их взаимодействии с перспективными конструкциями бесстыкового пути на железобетонных шпалах.
В соответствии с «Правилами расчетов верхнего строения железнодорожного пути на прочность» (утверждены МПС СССР 25.03.1954г.) при оценках динамического взаимодействия подвижного состава и железнодорожного пути рассматривается взаимодействие только неподрессоренной массы вагона и верхнего строения пути. Расчеты величины динамической добавки нагрузки колеса на рельс, выполняются без учета характеристик рессорного подвешивания вагона. В расчетах значения величин «взаимодействующих масс» задаются авторами, а не рассчитываются. Этот способ не позволяет оценить влияние допусков содержания рельсовой колеи на величины динамических добавок при разных механических характеристиках рессорного подвешивания вагона. Разгрузка колеса вагона при колебаниях, влияющая на безопасность движения вагона, не определяется.
Не учитывается неравномерное распределение нагрузки на колеса вагона, возникающее при его колебаниях при движении в кривых и в прямых.
Максимальные и минимальные нагрузки от разных колес вагона на рельсы при его движении могут отличаться более чем в три раза. В экспериментальных поездках у исследовательских вагонов-лабораторий ВНИИЖТ не все колеса вагона-лаборатории тензометрические. Кроме того, тензометрические колесные пары по своему устройству не позволяют получить объемную картину напряженно-деформированного состояния в контакте колеса и рельса.
На взаимодействие пути и подвижного состава влияют многие случайные факторы, не учитываемые при традиционных расчетах пути на прочность. Например, «Правилами…» [48] не учитывается уклон опорной площадки рельса и поперечный профиль колеса. Зарубежными исследователями [1] установлено влияние этих параметров на стабильность движения вагона в прямой.
Величины динамических добавок экспериментально исследуются ВНИИЖТ на скоростном полигоне Белореченская — Майкоп Северо-Кавказской железной дороги, но при анализе результатов экспериментальных поездок нельзя быть уверенным, что в месте установки датчиков отмечался максимум динамических воздействий. Вполне вероятно, что колесо вагона подойдет к датчику давления в фазе разгрузки. Устройство на пути системы искусственных неровностей, как это практикует ВНИИЖТ, для оценки максимумов давлений колес требует очень многих опытных поездок с широким спектром скоростей движения, с разной предысторией движения вагона перед неровностями и с учетом других факторов. Обычно эти требования в полном объеме невозможно выполнить и поэтому результаты опытных поездок по искусственно созданной системе неровностей на пути оказываются недостаточно представительными для многофакторного корреляционного анализа. Колебания подвижного состава — квазислучайный процесс, зависящий от многих факторов. Очень трудно в экспериментах обеспечить неизменное значение параметров железнодорожного пути по пути следования вагона, неизменность режима вождения поезда, учесть особенности каждой единицы подвижного состава. Поэтому, по данным экспериментов очень трудно оценить роль отдельных факторов, влияющих на колебания вагона.
До изготовления опытных образцов пассажирских вагонов и опытных конструкций железнодорожного пути вообще невозможно приступить к экспериментам, которые потребуют много времени и средств.
Для объективного исследования влияния допусков параметров рельсовой колеи на процесс колебания пути и подвижного состава при их взаимодействии необходимо моделирование взаимодействия вагона и пути с использованием полных моделей, учитывающих весь спектр механических характеристик системы пути и подвижного состава. Такие модели разработаны и уже более 10 лет применяются за рубежом. Они сертифицированы по международным стандартам ISO-9000/9001 (программные системы ADAMS/Rail, ANS YS, NASTRAN,COSMOS/M и т.д.).
Если в недалеком прошлом исследование взаимодействия пути и подвижного состава было делом опытным и расчетные коэффициенты динамики определялись экспериментально, то для новых конструкций пути и подвижного состава нового поколения уже можно с помощью сертифицированных программных систем решать нелинейные задачи о колебаниях подвижного состава и пути. Можно количественно оценить изменение технических требований к допускам содержания рельсовой колеи железнодорожного пути, по которому будут двигаться вагоны нового типа со скоростями более 140км/ч, чтобы при этом обеспечивалась безопасность движения поездов (устойчивость колеса на рельсе) и не возникали перенапряжения в элементах пути.
Возможная величина разгрузки колес определяет их устойчивость на рельсе и безопасность движения подвижного состава. Пока эта важнейшая характеристика исследована недостаточно, особенно, для условий скоростного движения пассажирских поездов. В 1996г. на Горьковской железной дороге на пути с хорошей или отличной оценкой при скоростях движения 40-80км/ч произошли без видимых причин сходы порожних газовых цистерн. По заданию МПС Российской Федерации ВНИИЖТ и НИЦ «Путь» Горьковской железной дороги выполнили испытания
аналогичных цистерн на участке пути Горьковской железной дороги Агрыз- Сарапул. Для примера на рис.28 показаны характерные поперечные ускорения вагонов, зафиксированные как на звеньевом, так и на бесстыковом пути.
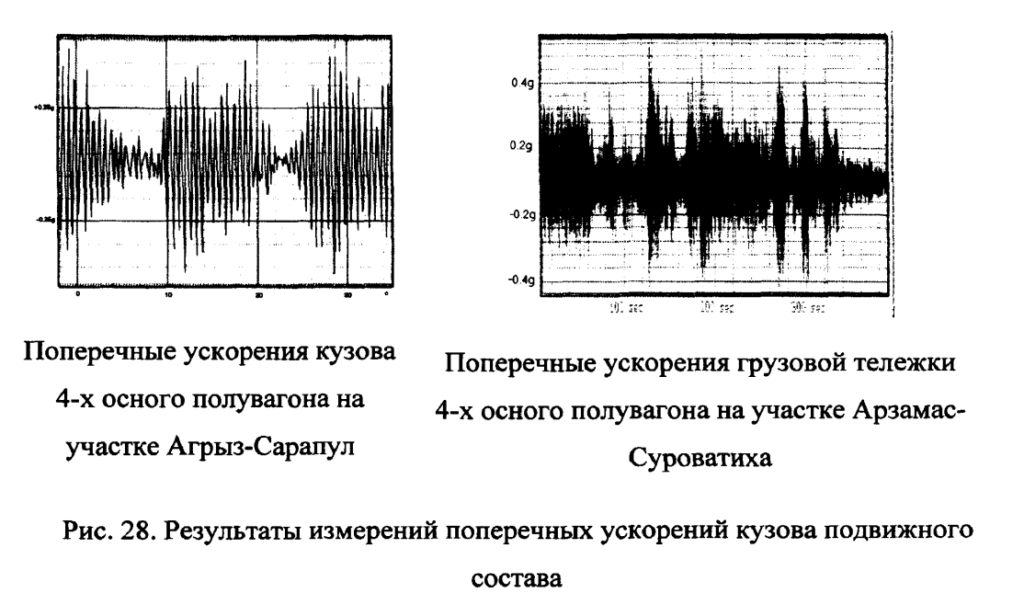
Как видно из анализа данных, приведенных на рис.28, колебания вагонов неизбежно сопровождают их движение по неровностям пути. Это естественный процесс, который формирует в сравнении со статикой нагрузкой перегрузки и разгрузки отдельных колес вагона.
Собственный вес вагона из-за колебаний распределяется между колесами неравномерно на прямых и в кривых. Обычно на колеса первой по ходу колесной пары приходится большая нагрузка. При этом, например, на правое колесо в какой-то фазе колебаний может приходиться 0.25 от статической осевой нагрузки, а на другое — левое колесо — 0.8. К рельсу от колеса прилагается не постоянная (статическая), а переменная (динамическая) нагрузка.
Процесс безотрывного качения колеса по рельсу нарушается не только в стыках, но и при определенных сочетаниях неровностей на пути и колесах. Тогда взаимодействие колеса и рельса приобретает ударный характер.
Проблема нуждается в решении на более качественной, чем это практиковалось ранее основе — рассмотрении в динамике взаимодействия пассажирского вагона нового поколения с бесстыковым путем перспективной конструкции. Решение этой проблемы для перспективных типов подвижного состава возможно на базе моделирования динамического взаимодействия с использованием программных систем, адекватно отображающих динамическое взаимодействия пути и подвижного состава.
Система экипаж-путь имеет много собственных частот. Когда одна из возбуждающих частот соответствует собственной частоте системы, возникают резонансные вибрации. В то время как собственные частоты рассматриваемой системы не зависят от скорости движения, вынуждающая частота, связанна со скоростью прохода шпал и с расстоянием между осями колесных пар в тележке.
Необходимо знать спектр частот собственных колебаний пути и спектр колебаний подвижного состава, чтобы исключить резонанс при их взаимодействии.
Краткий обзор теории механических колебаний
Колебательные процессы оказывают огромное влияние на условия эксплуатации железнодорожного пути, его прочность, устойчивость и долговечность. Разные по физической природе колебательные процессы описываются одинаковыми по форме уравнениями. Различают свободные и вынужденные колебания.
Свободные колебания — колебания автономных систем, происходят под действием восстанавливающих сил около состояния равновесия. Восстанавливающими называются силы, возникающие при отклонении системы от положения равновесия и направленные так, чтобы вернуть систему в это положение. В роли восстанавливающих обычно выступают появляющиеся при деформировании упругие силы, сила тяжести и сила Архимеда.
Вынужденные колебания поддерживаются внешними вынуждающими силами, зависящими от времени.
Характеристики свободных колебаний — собственные частоты и собственные формы, полностью определяют индивидуальные механические свойства системы.
Известно несколько способов составления дифференциальных уравнений колебательного движения. Наиболее общий — метод уравнений Лагранжа, но во многих случаях более удобен прямой метод записи уравнений движения, который применен в диссертации для расчета динамики взаимодействия вагона и железнодорожного пути.
Рассмотрим пример системы, состоящей из двух грузов, соединенных пружинами (рис.29).
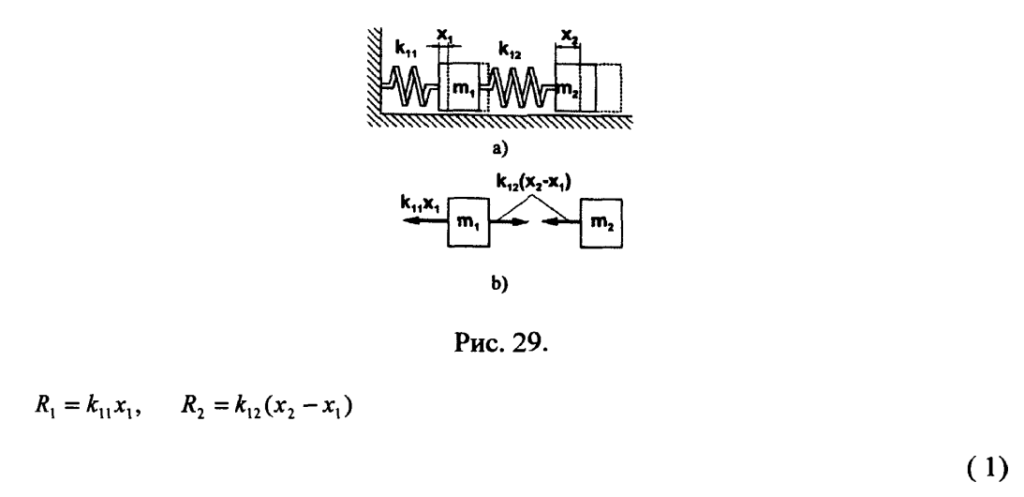
Дифференциальные уравнения движения грузов в соответствии со вторым законом Ньютона имеют вид:




перепишем (4) в матричной форме




или


Если все элементы матрицы демпфирования (14) положительны, то вещественные части всех корней характеристического уравнения (17) отрицательны. Каждому вещественному отрицательному корню р = -оа2 (в том числе и вещественной части комплексного корня) соответствует частное решение вида

Общее решение систем (13) является результатом линейного сложения частных решений (18) и (19).
Если система воспринимает действие внешнего возмущения, то дифференциальные уравнения движения перестают быть однородными. В качестве внешнего возмущения могут выступать силы или кинематические параметры, приложенные к некоторой части системы. Независимо от конкретной физической природы, возмущение является явной функцией времени.



Системы (24)-(25) решаются непосредственно алгебраическими методами. Однако физически более наглядным является способ разложения искомых амплитуд по собственным формам.
До последнего времени спектр собственных частот взаимодействия пассажирского вагона и бесстыкового пути перспективной конструкции не был получен, аналитическое выражение для этого спектра колебаний получить невозможно. Но при заданных характеристиках рессорного подвешивания вагона и упругих характеристиках железнодорожного пути решение может быть получено численными методами на ограниченном временном интервале.
Исходными данными для расчетов и анализа служат механические характеристики подсистем рассматриваемого вагона и фактические неровности пути, измеренные вагоном-путеизмерителем ЦНИИ-4, координаты пути с периодическими или изолированными неровностями.
Резонансные эффекты в колеблющейся системе могут приводить к катастрофическим воздействиям. Амплитуды колебаний при резонансе ограничиваются только силами трения. Так, при испытаниях порожних газовых цистерн (Горьковская железная дорога, 1996г.) — исправная цистерна отличалась устойчивостью движения во всем диапазоне скоростей, в то время как старые цистерны с неисправными фрикционными системами в определенном диапазоне скоростей (70-80км/ч) выходили на режим движения, отличающийся очень большими динамическими ускорениями (во всех направлениях), и находились практически на грани схода.
Для анализа необходимо получить полный набор собственных форм и частот колебаний вагона, чтобы выяснить опасные для него резонансные частоты, возбуждаемые неровностями на пути. Анализ результатов массовых численных расчетов взаимодействия пути и подвижного состава позволит обосновать технические требования к бесстыковому железнодорожному пути для скоростного движения. Прямое заимствование зарубежных норм невозможно из- за существенных различий в качестве рельсов, колес и различий технических требований по эксплуатации пути и подвижного состава в России и за рубежом.
Факторы, учитываемые в модели взаимодействия экипажа и пути в программной системе АОАМ8/КаИ
В диссертации использована модель взаимодействия пассажирского вагона и железнодорожного пути программной системы АВАМ8ЛШ1, учитывающая коничность колес, кривизну поверхности катания головки рельса, режимы вписывания тележки вагона в рельсовую колею в кривых, тип контакта колеса и рельса, боковой износе рельса и бандажа колеса, демпфирование в подвеске экипажа и в конструкции пути.
Тележка цельнометаллического пассажирского вагона Д47, широко распространенного на железных дорогах России, состоит из рамы, двух колесных пар типа РУ-950 с буксами, четырех надбуксовых подвешиваний, центрального подвешивания, надрессорной балки, гидравлических гасителей колебаний, тормозной рычажной передачи колодочного типа и шкворня. Рама тележки через буксовые пружины и шпинтоны связана с колесными парами, а с надрессорной балкой связь осуществляется посредством гидравлических гасителей и продольных поводков, которые удерживают балку от горизонтальных перемещений. Надрессорная балка опирается на комплекты пружин центрального подвешивания, которые подвешены к раме тележки при помощи шарнирно-маятниковой люльки. Нагрузка от кузова вагона передается на опорные скользуны надрессорной балки, от балки через комплекты пружин передается на раму тележки, от рамы тележки через шпинтоны и пружины надбуксового подвешивания на буксы и колесные пары. Колесные пары находятся в контакте с рельсом.
В модели выделяется две ступени подвешивания колесных пар и тележек: 1-я ступень- надбуксовое подвешивание, 2-я ступень — центральное подвешивание (рис.30).
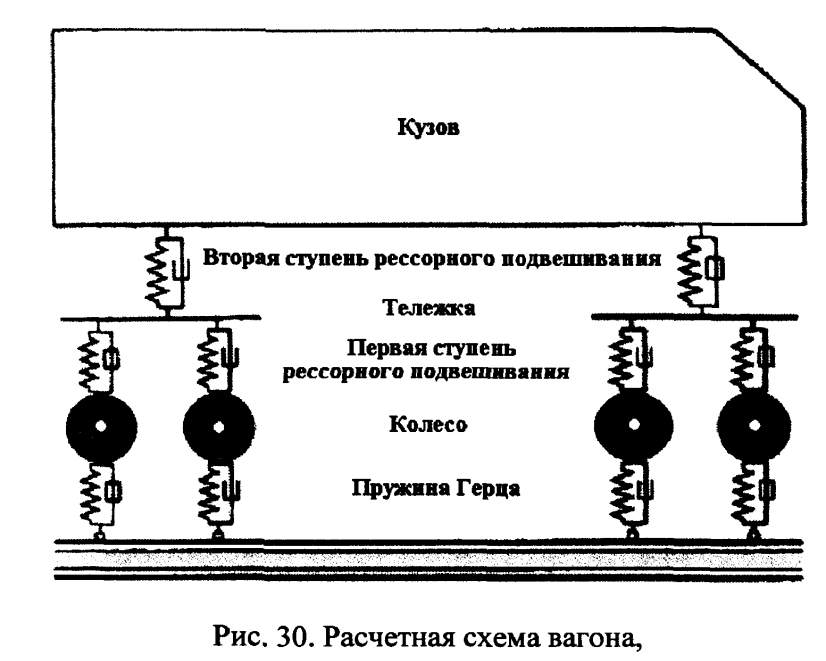
Расчеты выполнены для скоростного английского вагона типа ЕШИ, как возможного варианта конструкции скоростного вагона, и эксплуатирующегося на сети дорог МПС РФ цельнометаллического пассажирского вагона Д47, имеющего несколько больший вес кузова, другие размеры тележки и характеристики рессорного подвешивания.
В диссертации рассмотрено движение вагонов по: -переломам продольного профиля, -системе периодических неровностей, -изолированной неровности,
-по перекосам с разными расстояниями между вершинами и разной амплитудой вертикального отступления рельсовой колеи,
-участку звеньевого и бесстыкового пути.
Рассмотрено движение с разными длинами волн неровностей, когда колеса тележки оказываются в разной или в одной и той же фазе волны неровностей.
В качестве исходных данных о пути вводится файл описания рельсовой колеи (продольный профиль, вертикальные координаты, план линии, описание поперечного профиля головки рельса), файл описания поперечного профиля колес и файлы описания характеристик подсистем пассажирского вагона (кузов, тележки, колесные пары, рессорное подвешивание, демпферы, автосцепка и т.д.).
Взаимная ориентация колес и рельсов и принятые системы координат для колес и рельсов показаны на рис.32, левое и правое колесо вагона рассматриваются отдельно со своими системами координат. В расчетах учитываются отступления в геометрии рельса от правильной кривой или прямой (его геометрические отступления в плане и профиле от проектного положения). Учет отступлений в плане осуществляется смещением основания контактной площадки описывается параметром «и» (рис.33). На рис.34 приведены координатные системы и обозначены определяемые параметры, а также характеристики контакта колеса и рельса. На рис.35 приведены параметры контактирования колеса и рельса. Демпфирование колебаний определяется с учетом скорости деформации демпферов в соответствии с их нелинейными характеристиками (рис.38), возникающие в контакте колеса и рельса определяются по модифицированной теории Герца (рис.37).
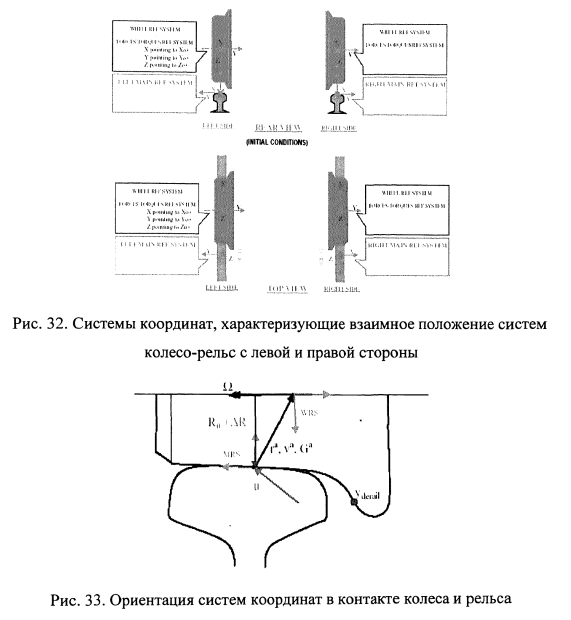
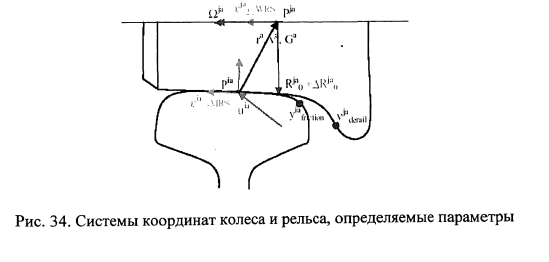
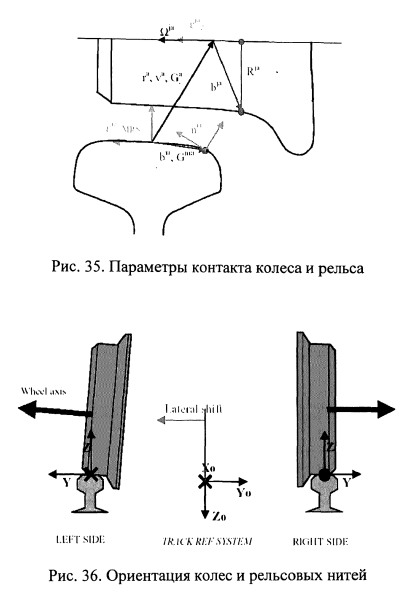
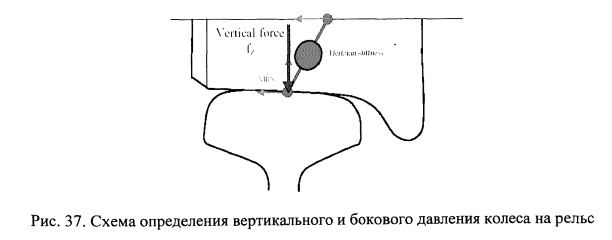
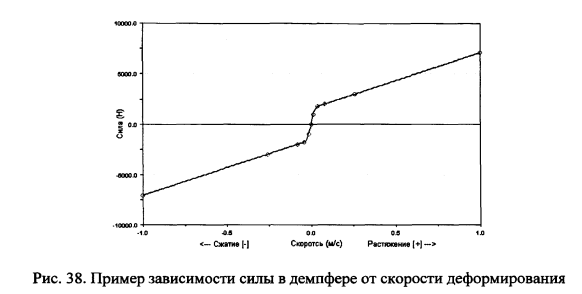
Ниже дано пояснение приведенных на рис.32-37 обозначений:


Расчет динамических показателей проведен для моделей контакта «Level 1» и «Level3» — модель De Pater — J.J. Kalker [3, 4, 6, 7]. Механическая колеблющаяся система экипаж-путь имеет 959 степеней свободы. Расчет параметров взаимодействия в процессе движения вагона за 20-30с требует около часа машинного времени при использовании персонального компьютера на базе Pentium-4/1.5GHz.
Расчет собственных форм и частот колебаний пассажирских вагонов
Эксплуатируемые и проектируемые для железных дорог России скоростные поезда предназначаются для сравнительно коротких по времени поездок (3-7часов) на расстояние 400-1000км. Вагоны таких поездов оборудуются комфортабельными креслами, они имеют меньший вес кузова, чем эксплуатируемый на сети цельнометаллический вагон Д 47, разделенный на купе и перевозящий меньшее количество пассажиров. Для оценки воздействий пассажирских вагонов на путь необходимо рассмотреть колебания эксплуатируемого пассажирского вагона и перспективного пассажирского вагона. На рис.39-40 показаны применяемые в Европе и Азии скоростные поезда и проектируемый для скоростных железных дорог России поезд. При длине одного вагона около 25м длина скоростного поезда составляет от 75 до 150м.
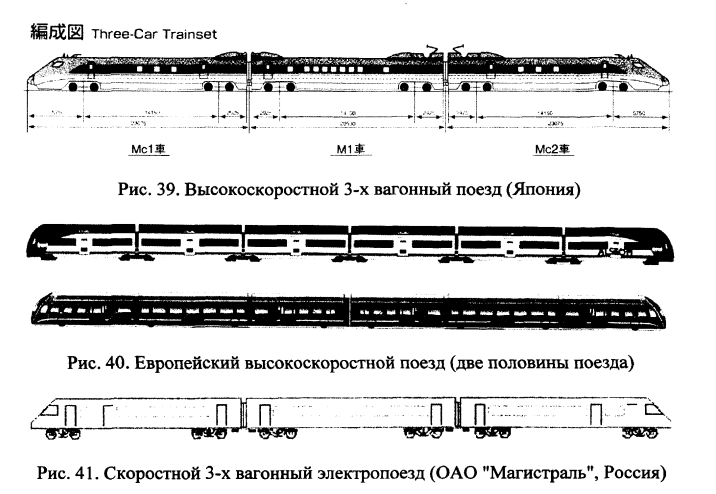
Отечественный скоростной вагон разработан ОАО ПКБВ «Магистраль» показан на рис.41. Характеристики колебаний этого вагона приведены в [22-23].
В японском высокоскоростном поезде (рис.39) максимальная статическая осевая нагрузка равна 12.25тс В отечественном скоростном поезде (скорость 160км/ч) (рис.41) статическая осевая нагрузка равна 16тс/ось.
Выполним расчеты собственных форм и частот колебаний цельнометаллического вагона типа Д47 (на базе которого сделан путеизмеритель ЦНИИ-4 с осевой нагрузкой 18тс/ось) и перспективных пассажирских вагонов (типа ЕМИ) с уменьшенной до 11-16тс/ось осевой нагрузкой.
Собственные частоты и соответствующие им формы колебаний обусловлены массами частей вагона и кузова, их размещением, моментами инерции, механическими характеристиками демпферов и жестокостями пружин рессорного подвешивания.
В таблице 6 приведены полученные нами в результате расчета модели вагона Д47 характеристики его собственных форм и частот колебаний. В таблице 5 приведены характеристики для облегченного пассажирского вагона, полученные расчетом в ПКБВ ОАО «Магистраль» [22-23] для вариантов с жестким и гибким кузовом вагона:
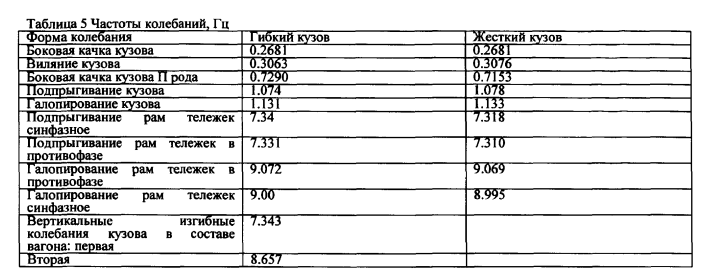
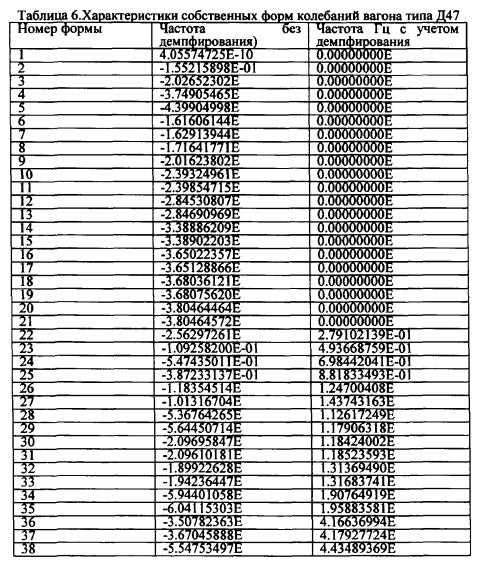
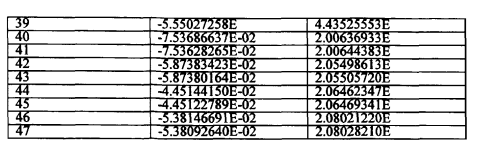
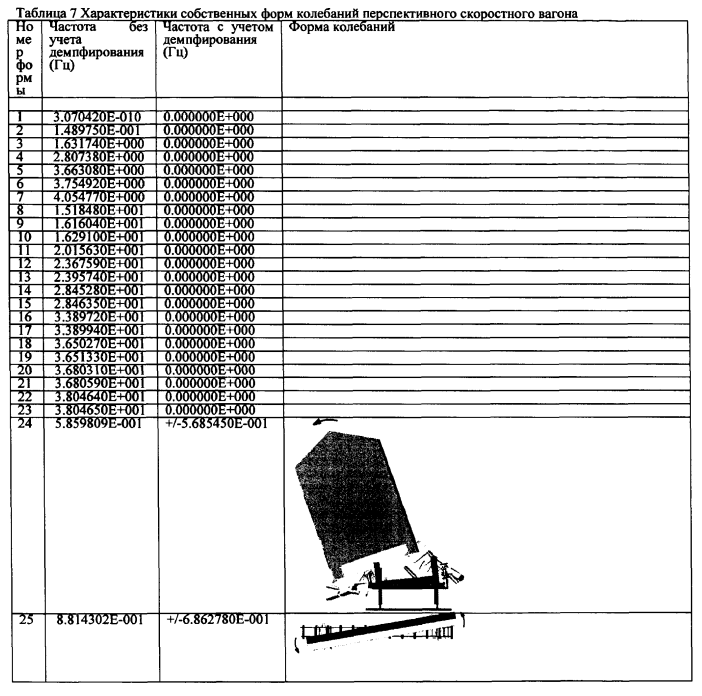
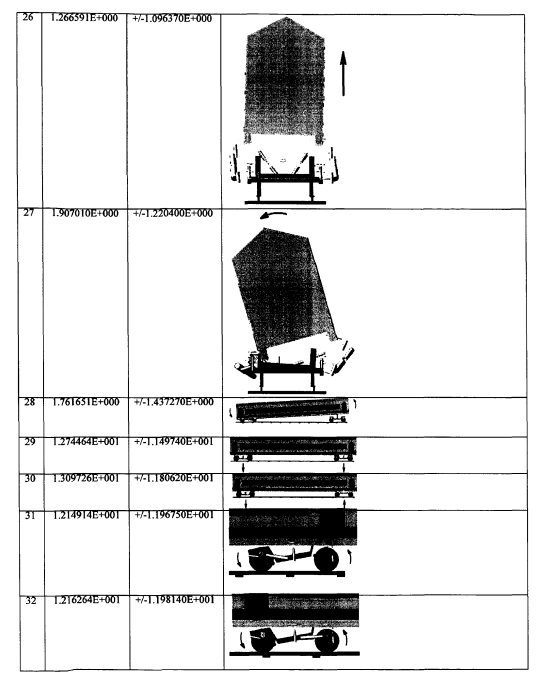
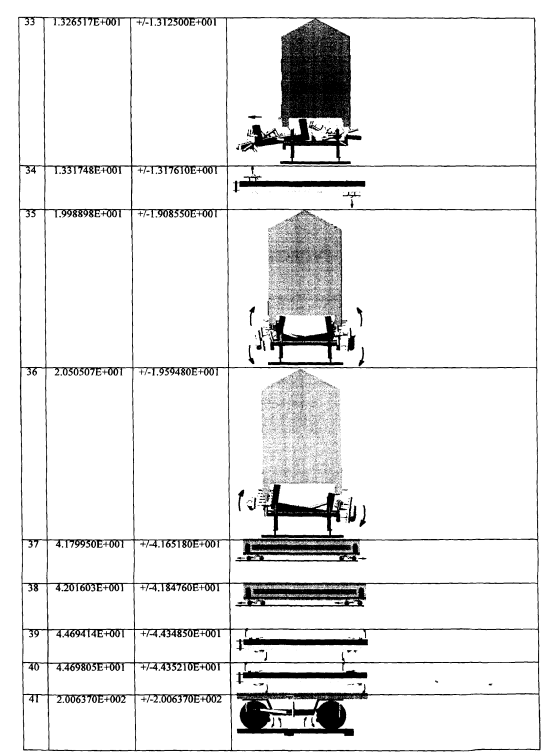
Анализ результатов расчетов частот и форм колебаний позволяет выделить три группы форм относящихся:
-к колебаниям кузова вагона, которые имеют частоту от 0.58 до 1.76 Гц,
-колебания тележки вагона с частотой от 12.7 до 44.7Гц,
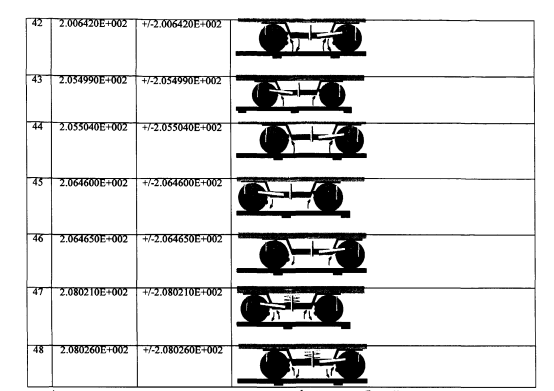
-вибрации колесной пары в буксовом узле от 200 до 208Гц, (приведены не демпфированные частоты).
Например, форма колебаний №26 отражает вертикальные перемещения кузова с частотой 1.27Гц, боковая качка кузова описывается формой №27 и имеет частоту 1.91 Гц, галопирование кузова происходит при частотах 12.6Гц (форма №28), при форме колебаний №33, имеющей частоту 13.27Гц, происходят поперечные оси пути смещения рам тележек вагона.
Более спокойный ход имеют вагоны, у которых большая часть собственных форм колебаний демпфированы. У вагона Д47 полностью демпфированы первые 21 форма колебаний (часть форм колебаний кузова и тележки), у перспективного скоростного вагона демпфированы полностью 23 первые формы.
Полученные характеристики собственных колебаний отдельных подсистем вагонов позволяют определить диапазон параметров неровностей железнодорожного пути в котором не происходит резонансных эффектов при движении вагона. С увеличением скорости приходится контролировать просадки и перекосы с большей длиной между вершинами. Чтобы исключить резонансные колебания тележек вагона при скоростях до 50м/с необходимо при выправке пути устранить просадки короче 5-10м.
Экспериментальные исследования колебаний пути при проходе скоростных и высокоскоростных поездов проведены в России и за рубежом. Установлено, что вибрации распространяются от пути через грунт в виде волн сжатия, поперечных и поверхностных волн (волны Релея). Для каждого типа волн энергия уменьшается по мере удаления от источника колебаний, так как она рассеивается на возрастающей площади и в результате материального поглощения. В земляном полотне наименьшие частоты поглощаются в минимальной степени.
По результатам измерения значений двух смежных (за один период) амплитуд колебаний А[ и А1+1 находится величина коэффициента поглощения колебаний:


По данным Эсвельда [74] основная часть энергии колебаний (до 67%) передается в виде поверхностных волн, а поперечные волны и волны сжатия
составляют около 26% и 7% соответственно. При скоростном движении поездов важно не допускать значительного роста частот и амплитуд колебаний, так как это связано с ростом уровня шума скоростных поездов.
Профессор И.В.Прокудин при замерах амплитуд и частот вынужденных колебаний пути [51] при пропуске скоростных и высокоскоростных поездов на Октябрьской железной дороге выделял низкочастотную, среднечастотную и высокочастотную гармоники колебаний пути.
Низкочастотные колебания характеризовались им на звеньевом пути частотой 1.8-2.5Гц и амплитудой до 140мк. Она проявлялась при скорости движения 130- 140км/ч и обусловлена колебанием цельнометаллического кузова пассажирского вагона. При проходе по участку локомотива она не регистрировалась, а при уходе состава с исследуемого сечения затухала практически мгновенно.
Среднечастотная гармоника обусловлена силовым воздействием вагонных тележек и характеризовалась частотой от 6 до 10Гц. В момент прохода осей вагона отмечался всплеск частотой 16-25Гц. Амплитуда колебаний достигала 90- 110мк.
Высокочастотные колебания колесных пар имели частоту от 30 до 200Гц и амплитуду 3-7мк. Волнообразный износ рельса (длина волн до 0.25м) вызывал вибрацию колесных пар в буксовом узле.
Результаты экспериментальных исследований на Октябрьской железной дороге не противоречат полученным нами расчетами с использованием комплекса АОАМЗ/ЯаП характеристикам колебаний вагона типа Д47.
Расчет воздействий на путь колес пассажирских вагонов при прохождении ими системы вертикальных периодических неровностей (просадок пути)
Разброс амплитуд неровностей просадок пути во многом определяется конструкцией пути и типом промежуточных рельсовых скреплений.
При упругом скреплении БПУ (рельсы Р65 и щебеночный балласт 30см под железобетонной шпалой) на Горьковской железной дороге максимальная амплитуда составила 2мм, при жестком скреплении КБ-65 (рельсы Р65 и щебеночный балласт 30см под железобетонной шпалой) амплитуда превышает 5мм, а в зоне стыков уравнительных пролетов она составляет 8-10мм и больше.
Рассмотрим влияние просадок пути на величину динамических добавок при взаимодействии колеса и рельса цельнометаллического пассажирского вагона и бесстыкового пути. Рассчитаем изменение величин динамических добавок сил в контакте колесо-рельс при прохождении цельнометаллическим вагоном непрерывных вертикальных синусоидальных неровностей. Выполним расчеты с такими длинами волн, когда одно колесо тележки находится в противофазе к другому (длина волны равна 1.2м) и когда оба колеса находятся в одной фазе (длина неровности равна расстоянию между осями колесных пар в тележках — 2.4м, вагон Д47).
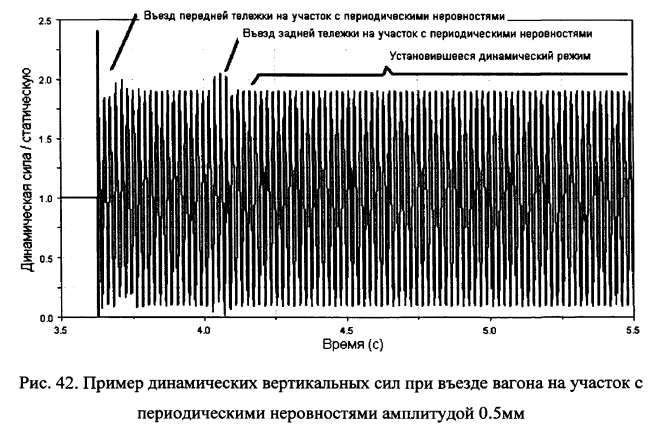
При въезде передних колес вагона на неровность (рис.42) виден всплеск динамической нагрузки колеса на рельс и интенсивная разгрузка колеса. После въезда всех колесных пар вагона на периодические неровности устанавливается динамическое равновесие, когда величина динамической нагрузки несколько спадает. В зависимости от частоты и амплитуды возмущений имеет место отрывное или безотрывное движение колеса по рельсу (рис.42-44).
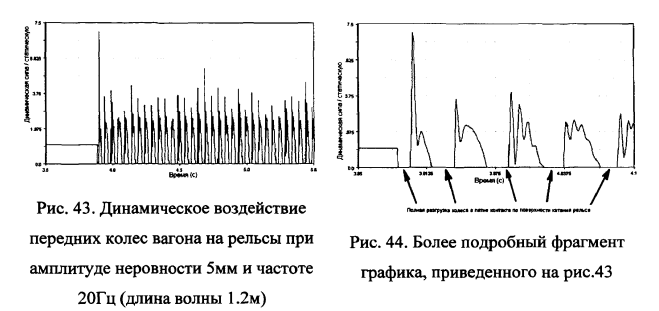
Как видно из анализа данных рис.43 увеличение амплитуды периодической неровности до 5мм приводит при частоте воздействия 20Гц к полной разгрузке отдельных колес и к большим их перегрузкам (в 3-5 раз больше статической нагрузки). Переход от безотрывного движения колес по рельсу к отрывному крайне нежелателен, так как при этом нагрузка от колеса на рельс носит ударный характер и увеличивается в несколько раз.
На рис.45 и в таблице 8 приведены результаты расчетов и кривые динамических нагрузок от колес, которые отражают спектр колебаний вагона от неровностей на поверхности катания рельса. Расчетная амплитуда в 0.5мм примерно на 50% меньше фактической у новых рельсов выпускаемых КМК и НТМК, но в три раза больше, чем нормируемая для скоростного движения и практикуемая за рубежом. По данным ВНИИЖТ средняя фактическая амплитуда неровности длиной 1м на поверхности катания отечественных рельсов равна 0.75мм. При амплитуде синусоидальной непрерывной неровности с амплитудой в 0.5мм демпфирующая система вагона справляется с гашением колебаний даже при частоте воздействия в 50Гц и движение колес по рельсам остается безотрывным.
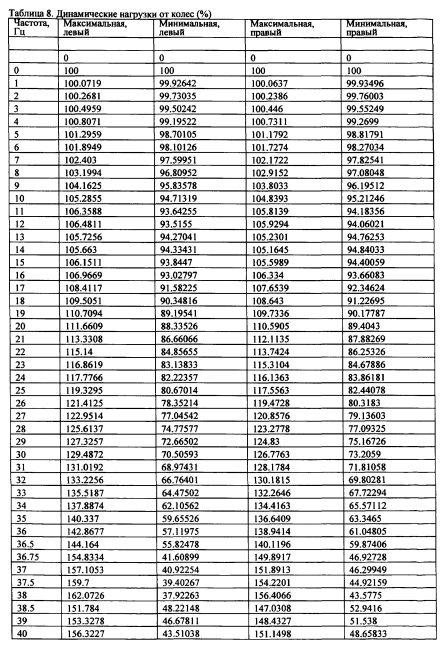
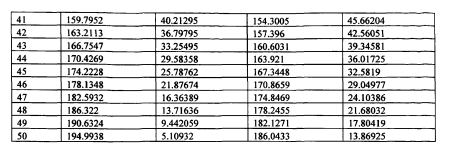
Увеличение амплитуды неровности приводит к нарушению условия безотрывного движения колеса по рельсу на более низких частотах.
Рассмотрим далее влияние просадок пути с большими чем 0.5мм амплитудами, не превышающими величины просадок первой степени: 2мм — соответствующие упругому промежуточному рельсовому скреплению БПУ и 6мм — соответствующие скреплению КБ-65 с жесткой П-образной клеммой. Результаты расчетов динамических вертикальных сил для периодических просадок с длиной волны 1м приведены на рис.46 .
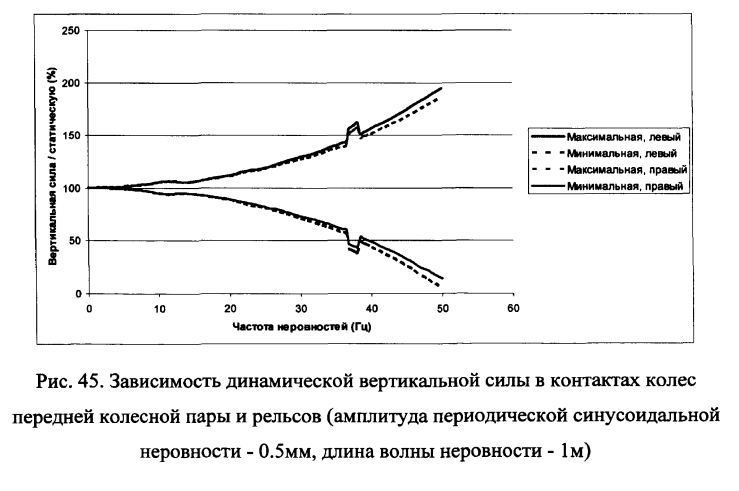
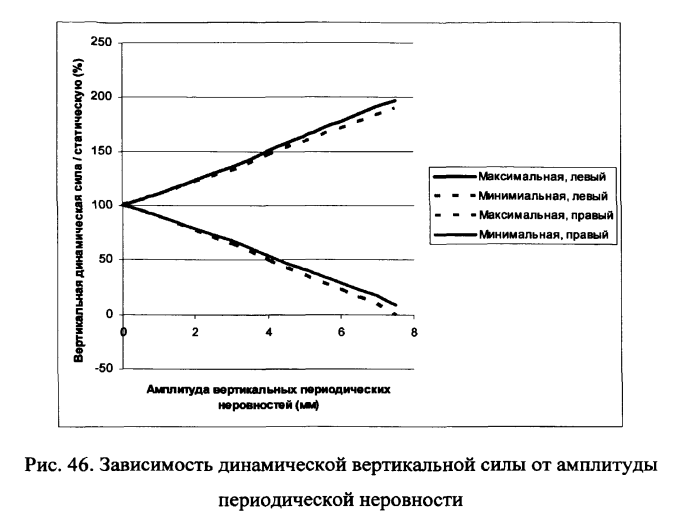
Увеличение скорости движения поездов требует снижения амплитуды неровностей и увеличения их длин. Допускаемые неровности при скоростном движении должны быть более пологами. В диссертации это требование впервые получило теоретическую количественную оценку для конкретного типа подвижного состава.
Движение вагона через изолированную неровность
Рассмотрим прохождение вагоном типа Д47 одиночной изолированной синусоидальной неровности амплитудой 0.5мм и длиной 1м. Результат расчета динамических нагрузок приведен на рис.47 в сравнении с прохождением системы периодических неровностей.
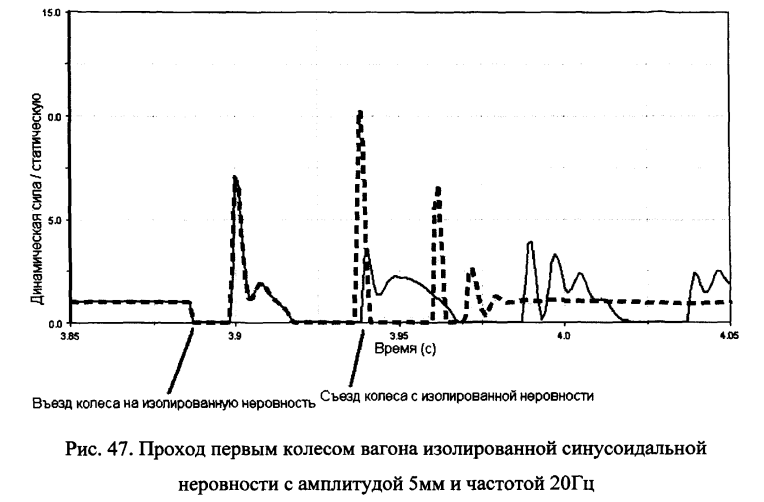
Как видно из сравнения данных расчета при прохождении одиночной неровности (где фиксируются всплески нагрузок и динамическое равновесие не успевает наступить) при данном сочетании параметров величины динамических нагрузок на путь выше, чем при проходе регулярных неровностей. При данном сочетании параметров при прохождении синусоидальной изолированной неровности с большой амплитудой происходит большее нагружение пути на выходе из неровности, чем при установившемся динамическом равновесном движении вагона по системе периодических неровностей с той же амплитудой. Сегодня есть техническая возможность ужесточения требований к отступлениям рельсовой колеи, так как компьютеризованные рихтовочные системы на машинах ВПО и ВПРС, Дуоматик и Унимат обеспечивают отклонения положения рельсовой колеи от проекта не более 1мм при использовании лазерных визиров и специальных тележек, устанавливаемых в местах перелома продольного профиля.
Движение колес вагона в кривых
Выполним расчеты вертикальных нагрузок колес на упорный и внутренний рельс в кривой для рельсовой колеи без отступлений при колесах вагонов без отступлений по геометрии. В качестве примера, на рис.48-52 приведены некоторые результаты расчетов вертикальных и боковых сил с использованием системы АОАМ8/И.аП для движения пассажирского вагона по кривой радиуса 1500м и примыкающим прямым участккам, (возвышение наружного рельса — 40мм, скорости — 10-70м/с).
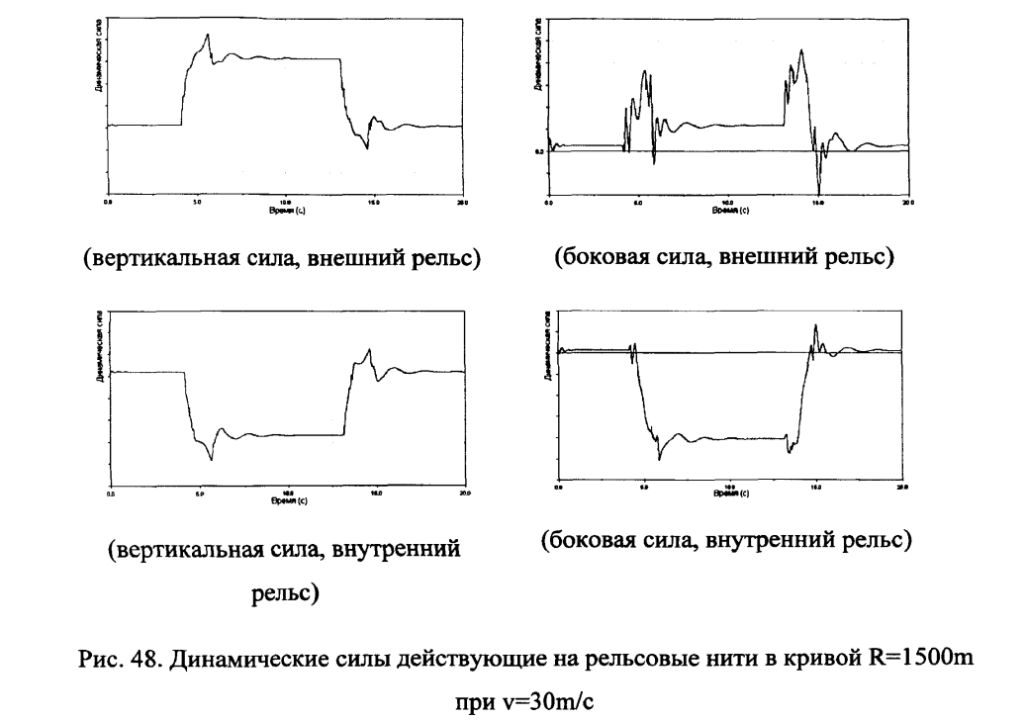
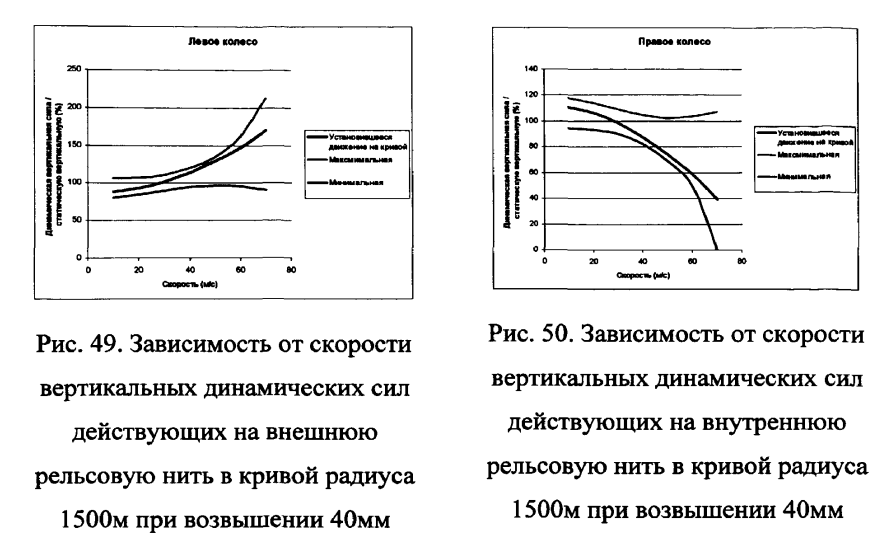
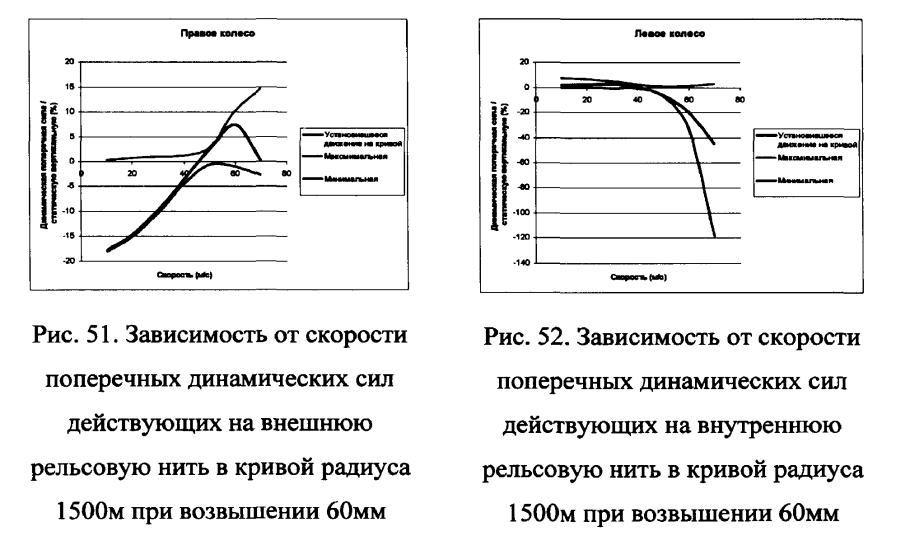
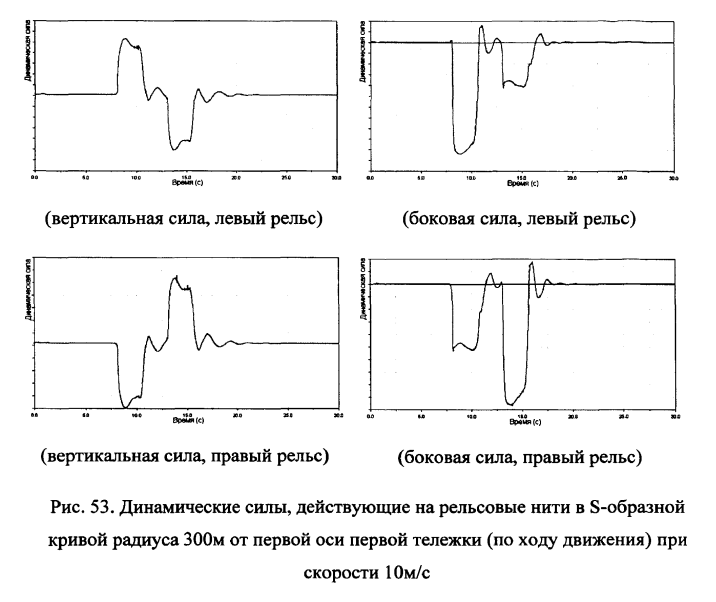
Для оценки изменения силового воздействия вагона на путь при вписывании в круговую и обратные кривые выполнен расчет прохождения Б-образной кривой радиусом 300м, соответствующей движению на боковой путь по стрелочному переводу марки 1/11 (рис.53).
Допуская уровень безопасной минимальной нагрузки на внутренний рельс и максимальных нагрузок на внешний рельс можно определить допускаемую скорость движения в кривой.
Движение вагона при периодически изменяющейся ширине колеи в прямой
Ширина колеи в прямых и кривых постоянно меняется в пределах, зависящих от конструкции пути. Для пути на железобетонных шпалах эти пределы могут быть более 5 мм из-за допусков при изготовлении железобетонных шпал и монтаже рельсошпальной решетки.
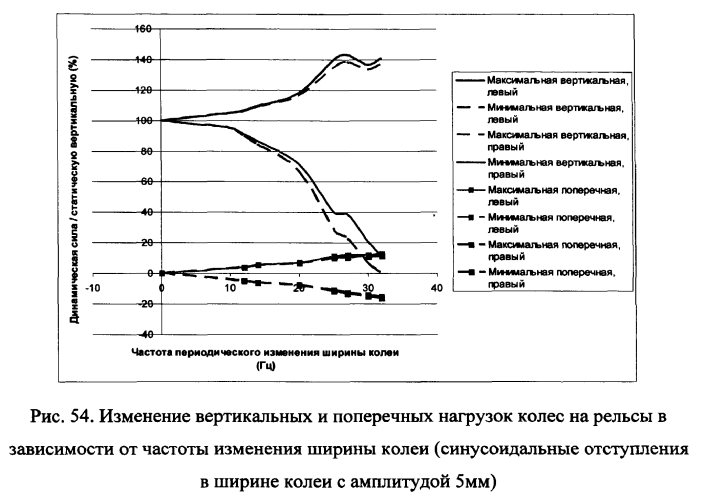
Рассмотрим влияние частоты изменений ширины колеи на величину возникающих от этого вертикальных и поперечных сил. На рис.54 приведены результаты расчетов для амплитуды в ±5мм синусоидального периодического изменения ширины колеи. Как видно из анализа данных рис.54 уширение и сужение колеи влияют в большей степени на разгрузку одного из колес и с увеличением частоты до 25Гц эта разгрузка становится опасной с позиции устойчивости колеса на рельсе. При амплитудах изменения ширины колеи в пределах 1-2мм динамические вертикальные и поперечные силы незначительны.
Так как введение скоростного движения приводит к увеличению частоты воздействий неровностей на пути, необходим выбор подкладочной конструкции пути и более тщательная сборка решетки, чтобы при максимальной скорости движения частота изменения ширины колеи была не более 10Гц.
Влияние перекосов пути на вертикальные давления колес на рельсы
Выполним расчет воздействия колесных пар на рельсовые нити при прохождении системы перекосов. Рассмотрим перекос (две изолированные неровности по разным рельсам с длиной волны 4м, амплитудой 0.5мм и расстоянием между вершинами 20м). Результаты расчетов приведены на рис.55-56.
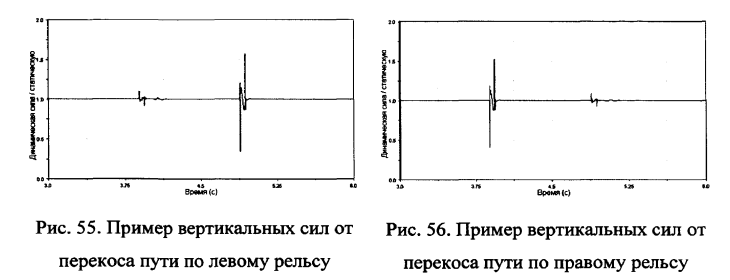
Малые амплитуды (0.5мм) при большом расстоянии между вершинами перекоса и сравнительно малой скорости движения приводят к независимому действию колесных пар на неровности по правому и левому рельсам.
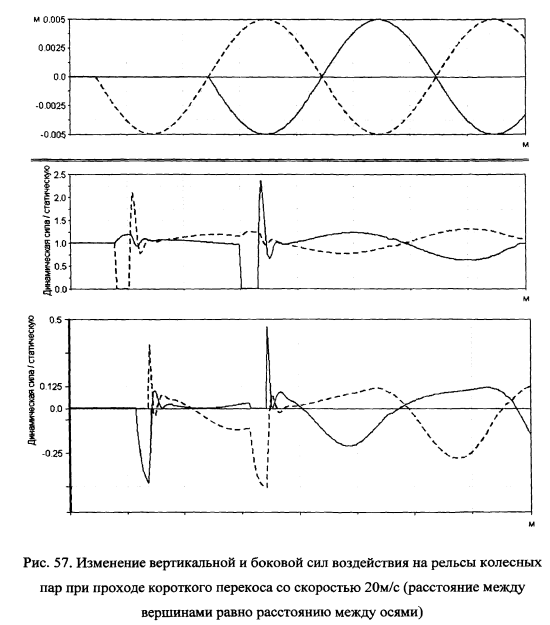
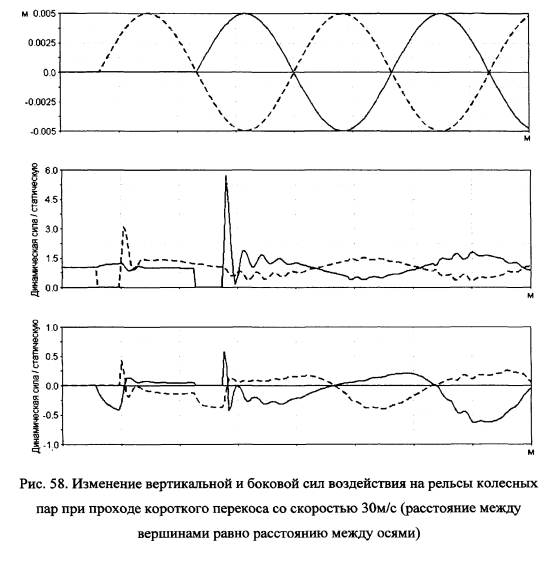
При увеличении скорости движения до 30 и 40м/с происходит увеличение вертикальных и поперечных компонент нагрузки колеса на рельс и увеличивается длина участка отрывного движения колеса. При скорости 40м/с вертикальная компонента нагрузки превосходит статическую нагрузку в 8 раз, а поперечная сила превосходит статическую вертикальную в 1.75 раза. Короткие перекосы на скоростном участке пути должны устраняться при выправке пути.
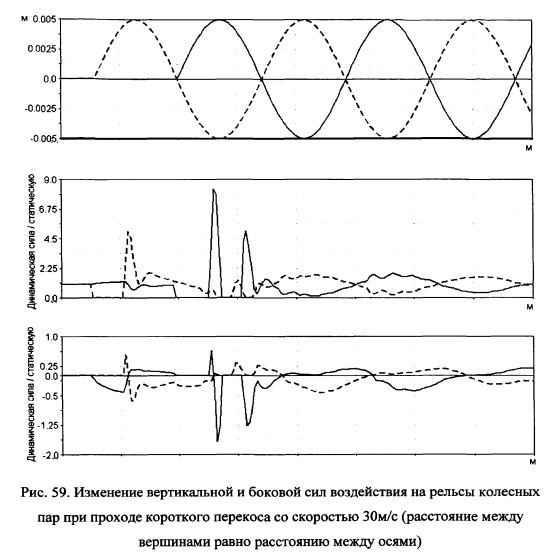
На рис.60 показано прохождение перекоса амплитудой 5мм при расстоянии между вершинами перекоса в 10м и скорости 40м/с. Такие перекосы отнесены к первой степени и не штрафуются, однако, как видно из данных рис.60 прохождение такого перекоса со скоростью 40м/с приводит к полной разгрузке колеса и к значительному росту динамической вертикальной силы. Такие перекосы при скоростном движении недопустимы, что должно быть учтено в нормативе по подготовке пути к скоростному движению.
Влияние амплитуды перекоса и частоты воздействия перекосов на пути на динамическую перегрузку и разгрузку колес вагона показано на рис.61.
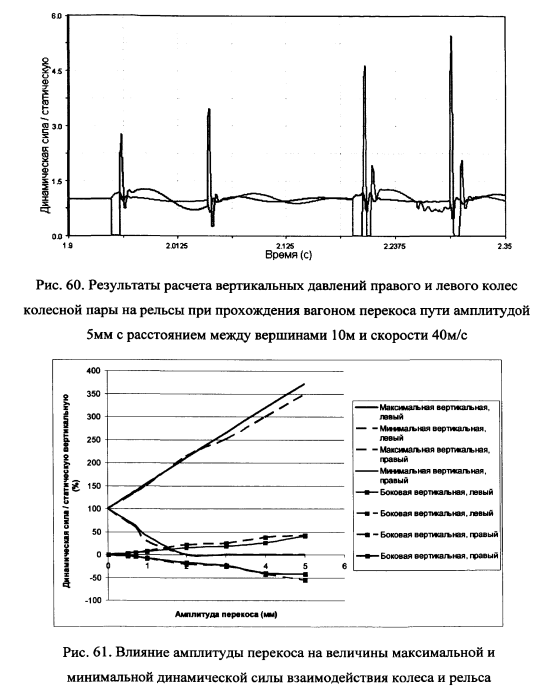
Влияние амплитуды перекоса на величины максимальной и минимальной динамической силы взаимодействия колеса и рельса
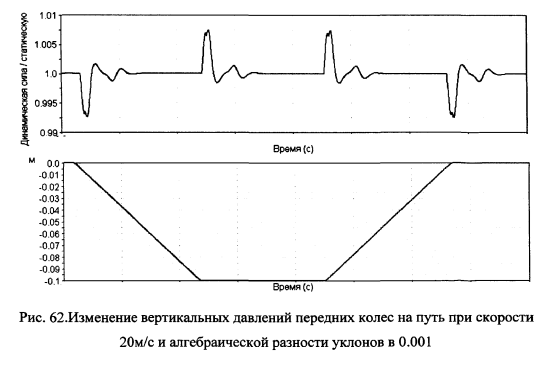
Скоростные поезда обычно имеют сравнительно небольшую длину (от 75 до 200м). В этом случае общее требование проектирования продольного профиля о размещении половины длины поезда на элементе профиля делает достаточной минимальную длину элемента равной 100м. Рассмотрим с помощью расчетов дополнительных динамических сил влияние алгебраической разности сопрягаемых уклонов на плавность движения. Ранее нами был предложен критерий, согласно которому при входе вагона на сопряжение элементов продольного профиля круговой кривой динамическая добавка не должна быть более 0.25 от статической осевой нагрузки.
Выполним расчеты динамических сил при скоростном движении вагона по участкам сопряжения уклонов продольного профиля пути.
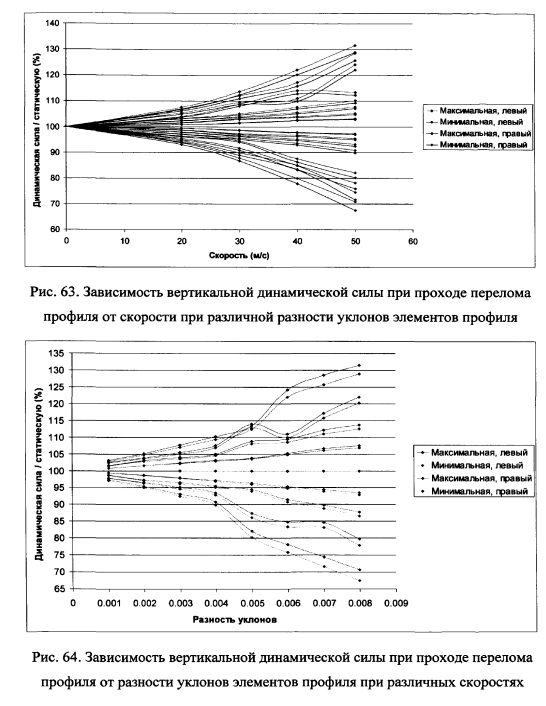
Выводы
Расчеты показали, что фактические перегрузки (динамические добавки) при скоростном движении в действительности больше по величине, чем рекомендуемые «Правилами расчета пути..», применяемыми при скоростях движения до 140км/ч. Ссылки на то, что измеренные за рубежом величины динамических добавок при скоростях до 200км/ч находятся в пределах 40-60% от статической нагрузки не могут применяться для отечественных железных дорог, где иная амплитудно-частотная характеристика неровностей пути.
Для пассажирского вагона нового поколения с заданными характеристиками на бесстыковом железнодорожном пути перспективной конструкции в диссертации выполнены расчеты собственных форм и частот колебаний.
Получены зависимости сил взаимодействия пути и подвижного состава при различных величинах отступлений в содержании рельсовой колеи. На основе анализа результатов моделирования движения перспективного пассажирского вагона установлена необходимость регламентировать допуски в содержании рельсовой колеи (просадок и отступлений ширины колеи) не только по амплитуде, но и по длине неровностей.
Установлено, что величина динамической нагрузки на путь при прохождении вагоном неровностей пути определяется амплитудно-частотной характеристикой возмущающей нагрузки. Задача службы пути при подготовке пути к скоростному движению заключается в недопущении коротких просадок и перекосов при выправке пути.
- При скоростном движении поездов со скоростями более 140км/ч требуется соблюдение более жестких нормативов содержания рельсовой колеи и применение более надежных конструкций железнодорожного пути, позволяющих соблюдать такие требования.
- Для обеспечения безотрывного качения колеса по рельсу при скоростном движении пассажирских поездов необходимо не допускать просадок пути более 1 степени по Инструкции ЦП774. На Горьковской железной дороге такие параметры выдерживаются только на пути со скреплениями БПУ, на пути с модернизированным скреплением КБ-65 (с клеммой ОП 511).
- В связи с малой длиной скоростных поездов длина элемента продольного профиля обычно не является лимитирующей при подготовке пути к скоростному движению. Принятому уровню динамических добавок соответствует алгебраическая разность уклонов элементов продольного профиля длиной не менее 100м не более 0.004. Радиус вертикальной кривой, сопрягающей элементы продольного профиля, при этом не должен быть менее 7500м.
- Утвержденные Департаментом пути в 2002г. правила приемки пути после выправки ЦПТ-55/2002, разрешающие до 15 просадок второй степени на 1км, для участков скоростного движения требуется откорректировать.
- Для уменьшения сил взаимодействия колеса и рельса нужно избавиться от коротких неровностей на поверхности катания рельса (пробоксовин на поверхности катания головки рельса, углов между сваренными рельсами и т.д.), что достигается шлифовкой рельса.
- При скоростном движении необходимо обеспечить плавность отводов отклонений рельсовой колеи. Анализ результатов проведенных расчетов сил взаимодействия колеса и рельса при прохождении неровностей пути показал, что требуемой является крутизна отвода не круче 1мм на 1м.
Список литературы
- Глюзберг Б.Э., Тейтель А.М., Титаренко М.И., Хвостик М.А. Новая конструкция контррельса-протектора / Вестник ВНИИЖТ, №3, 1997.
- Гончарук B.JI. Динамическая модель трехвагонного пассажирского электропоезда // Сборник трудов 2-ой конференции CAD-FEM, Москва,.2002. Стр.357-361.
- Гончарук B.JL, Новожилов Д.А. Оценка динамики прицепного вагона пассажирского электропоезда с учетом гибкости кузова // Сборник трудов 2-ой конференции CAD-FEM, Москва,.2002. Стр.362-367.
- Грачева Л.О. Взаимодействие вагонов и железнодорожного пути (вынужденные колебания вагонов)Лр. ВНИИЖТ, 1972, вып. 356. 207с.
- Грищенко В.А. Обеспечение надежности и эффективности бесстыкового пути в сложных условиях эксплуатации. Москва, ВНИИЖТ, 1992.
- Данилов В.Н. Расчет рельсовой нити в зоне стыка./ Труды ВНИИЖТ. Вып. 70. М., Трансжелдориздат, 1952, 113с.
- Ермаков В.М. Эффективность удлинения рельсовых плетей // Путь и путевое хозяйство, №5, 1998. Стр.7-9.
- Железнодорожный путь./ Т.Г.Яковлева, Н.И.Карпущенко, С.И.Клинов, Н.Н.Путря, М.П.Смирнов. Под ред. Т.Г.Яковлевой. М., Транспорт. 1999. 405с.
- Жинкин Г.Н., Прокудин И.В. Изменение прочностных характеристик глинистых грунтов при действии вибродинамической нагрузки и его влияние на устойчивость земляного полотна. В кн.»Свойства грунтов при вибрациях. Материалы третьей Всесоюзной конференции.» Ленинград, 1973, с. 164-170.
- Задорожный Л.И., Исаенко Э.П., Русин А.Н., Безруков М.В. Совершенствование конструкции и технологии текущего содержания бесстыкового пути: Пособие. Н.Новгород, изд. НГМА, 1999, 112с.
- Зенкевич О. Метод конечных элементов в технике. Москва, Мир, 1975. 541с.
- Иванов С.Ю., Исаенко Э.П., Безруков М.В. Подготовка железнодорожного пути к скоростному движению пассажирских поездов: Пособие. Нижний Новгород, Горьковская железная дорога, «Нижегородский печатник», 2001,136с.
- Каменский В.Б., Шац Э.Я. Содержание железнодорожного пути в кривых. М.,Транспорт, 1987, 189 с.
- Карпутценко Н.И. Надежность связей рельсов с основанием. Москва, Транспорт, 1986. 150с.
- Карпущенко Н.И., Иванова Л.И. Упругие продольные перемещения
рельсов под воздействием подвижной нагрузки./Сб. науч. Тр./ НИИЖТ, 1977.Вып.185. с.47-55. - Коган А .Я. Динамика пути и его взаимодействие с подвижным составом. 1997.
- Коган А .Я., Грищенко В.А., Косенюк В.К. Устойчивость бесстыкового пути при температурном воздействии // Обеспечение надежности и эффективности бесстыкового пути в сложных условиях эксплуатации. Новосибирск: 1991. Стр.5-15.
- Коган А.Я., Пейч Ю.Л. Расчет нестационарного напряженно- деформированного состояния элементов конструкции пути в зоне стыка рельсов. Вестник ВНИИЖТ, 2/2002, с.31-39
- Конечно-элементные модели расчета железнодорожного пути на прочность и устойчивость: Сб. ст. / Ауезбаев Е.Т., Безруков М.В., Васильев А.Б., Васильев С.П., Исагалиев Е.Б. Исаенко Э.П. Под ред. Э.П.Исаенко. Калининград, Гудок, 1997. 136с.
- Крейнис З.Л. Спектральный состав очертания рельсовых нитей./Вестник ВНИИЖТ, 1982, №4, с.48-51.
- Кудрявцев И.А. К вопросу о виброперемещениях, возникающих в земляном полотне // Устойчивость геотехнических сооружений на железнодорожном транспотре. Днепропетровск, 1989, стр.79-84.
- Лазарян В.А., Литвин И.А. Дифференциальное уравнение колебаний экипажа, движущегося по инерционному пути. / Сб. «Некоторые задачи механики скоростного транспорта» Киев. Наукова думка. 1970, с.61-73.
- Методические рекомендации по оценке инвестиционных проектов на железнодорожном транспорте. Утверждены указанием МПС России № В- 1024у от 31.08 1998г.
- Методические рекомендации по оценке эффективности инвестиционных проектов (вторая редакция). Утверждены Минэкономики России, Госкомитетом России по строительной, архитектурной и жилищной политике №ВК477от21.06.1999г.
- Першин С.П. Радиусы кривых при высокой скорости // Путь и путевое хозяйство, №1, 1998.
- Попов С.Н. О допускаемых напряжениях на балласт / Вестник ВНИИЖТ, №97. Москва, 1955. Стр.353-385.
- Правила расчета пути на прочность и надежность в зависимости от класса путей. ВНИИЖТ МПС, Москва, 1999. 62с.
- Правила расчетов верхнего строения железнодорожного пути на прочность, МПС СССР 25.03.1954г.
- Приказ министра путей сообщения №12Ц от 16.08.94г «О переходе на новую систему ведения путевого хозяйства на основе повышения технического уровня и внедрения ресурсосберегающих технологий»/МПС РФ.М., 17с.
- Проблемы улучшения динамических свойств пути высокоскоростных магистралей // Ж.д. мира, №6, 1997.